flèche de retour

Physagreg

Cours de physique chimie

icone sommaireSommaire
icône cadeauBonus
icône chapitreAutres chapitres

Licence 1 > Thermodynamique > Cours 1 : grandeurs thermodynamiques et équations d'état

T3 : interprétation microscopique

Introduction

La thermodynamique étudie les échanges d'énergie à travers le travail et la chaleur a une échelle macroscopique, on étudie souvent une enceinte dans laquelle baigne un fluide, on décrit alors l'évolution des variables d'états, pression, volume, température, etc.
Quels sont les liens de ces variables au niveau microscopique, à l'échelle d'une molécule de fluide ? essayons de répondre à cette question dans ce chapitre.

Ordre de grandeur

Distribution des vitesses de Maxwell-Boltzmann

On va chercher ici à définir la vitesse quadratique moyenne, dont on va se servir pour calculer la pression cinétique, c’est à dire l’expression de la pression dans le cadre de l’interprétation microscopique d’un gaz.

Pour cela on fait appel à la physique statistique, domaine fondé par Boltzmann à partir de 1872. C’est Maxwell qui établit la loi qui donne les vecteurs vitesses des particules d’un gaz à l’équilibre thermodynamique : il s’agit d’une loi normale. Ainsi, on peut tracer l’allure de la distribution des vitesses :

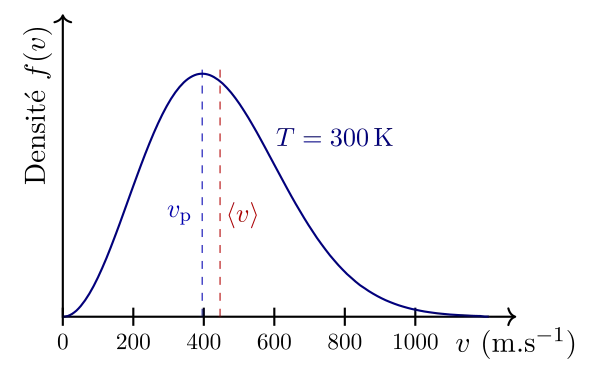
Distribution de Maxwell à T=300 K
Densité de probabilité pour une particule d’avoir la vitesse $v$
Distribution de Maxwell pour plusieurs températures
Allure de la distribution de Maxwell-Boltzmann en fonction de la température

Sur le graphe de gauche, la distribution des vitesses est donnée avec en ordonnée la densité de probabilité pour qu’une molécule ait une certaine vitesse et en abscisse la vitesse en question. On dispose alors, pour une température de 300 K, d’un ordre de grandeur des vitesses des molécules, ainsi que la valeur de la vitesse la plus probable $v_p$ et de la vitesse moyenne des molécules $\langle v \rangle$. On peut noter que cette courbe n’est pas symétrique.

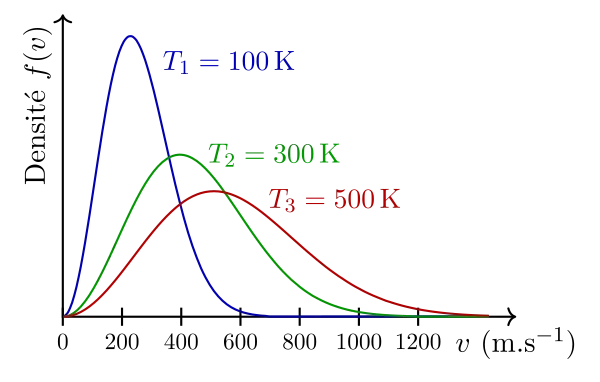
Sur le graphe de droite, la distribution des vitesses a été tracée pour différentes températures : on observe un aplatissement de la courbe au fur et à mesure que la température s’accroit, et un décalage de la vitesse la plus probable vers les hautes vitesses.

Donnons la forme mathématique de cette fonction. Pour cela, on s’intéresse à la densité de probabilité $f(v)$ dont l’intégrale donne la probabilité d’avoir une molécule qui a la vitesse $v$ comprise dans un certain intervalle : \begin{equation}f(v) = \mathrm{cste}\times\,v^2\,e^{-\dfrac{m\,v^2}{2\,k_B\,T}} \qquad \text{et} \qquad P(v_1\le v \le v_2) = \int_{v_1}^{v_2} f(v)\,\mathrm{d}v\end{equation} avec $m$ la masse d’une molécule de gaz, et $T$ la température de celui-ci. La densité de probabilité dépend d’une constante importante de la physique statistique, la constante de Boltzmann $k_B$.

La constante qui apparaît est une constante de normalisation, calculée afin que \begin{equation}\int_0^\infty f(v)\,\mathrm{d}v = 1\end{equation}

Cette distribution permet de calculer si on le souhaite la vitesse la plus probable (dérivée de la densité de probabilité qui s’annule), ou bien la vitesse moyenne $\left(\langle v \rangle = \displaystyle\int_O^\infty v\,f(v)\,\mathrm{d}v\right)$ ou encore la vitesse quadratique moyenne $\left(u=\sqrt{\langle v^2 \rangle} = \sqrt{\displaystyle\int_O^\infty v^2\,f(v)\,\mathrm{d}v}\right)$.

Vitesse quadratique moyenne

Focalisons nous sur cette dernière grandeur puisqu’elle va intervenir dans le calcul de la pression cinétique. On peut donc la définir de plusieurs manières :

En effet, l’intérêt de cette grandeur est lié à l’isotropie de l’espace : les molécules se déplacent indifféremment dans toutes les directions de l’espace, ainsi en moyenne, lorsqu’une particule se déplace dans le sens des $x$ croissants, une molécule se déplace dans le sens des $x$ décroissants si bien que $\langle v_x \rangle = 0$.

Deux raisons pour lesquelles on s’intéresse plutôt au carré des vitesses :

Selon l’isotropie de l’espace, on peut écrire \begin{equation}\langle v_x^2 \rangle = \langle v_y^2 \rangle = \langle v_z^2 \rangle = \dfrac{1}{3}u^2\end{equation}

Pression cinétique

On va s’intéresser ici à l’impact mécanique des molécules sur les parois d’une enceinte qui constitue la grandeur pression. Celle-ci étant le rapport d’une force sur une surface, en utilisant les notions de chocs élastiques en mécanique et de relation fondamentale de la résultante cinétique, on parvient assez vite à une expression.

On considère une molécule de gaz qui se dirige sur un morceau $\mathrm{d}S$ de paroi de l’enceinte qui le contient. On travaille pendant un intervalle de temps $\mathrm{d}t$. Pour simplifier le problème :

D’après la mécanique des chocs élastiques, il y a conservation:

Alors, la masse de la paroi étant bien plus grande que la masse d’une particule, une particule qui percute horizontalement la paroi avec un vitesse $\overrightarrow{u}$, est renvoyée avec la vitesse $-\overrightarrow{u}$.

Voici un schéma de la situation :

Pression cinétique : mise en situation
Choc d’une molécule de vitesse $u$ sur la paroi de l’enceinte

Comptage des molécules : pendant le temps $\mathrm{d}t$, les molécules qui peuvent percuter la paroi sont celles contenue dans un cylindre de base $\mathrm{d}S$ et de génératrice $u\,\mathrm{d}t$. Si on note $n^*$ le nombre de particules par unité de volume alors on un nombre de particules percutant la paroi égal à \begin{equation}\mathrm{d}N = \dfrac{1}{6}\,n^*\,u\,\mathrm{d}t\,\mathrm{d}S\end{equation}

Variation de quantités de mouvement : Calculons la variation de quantité de mouvement d’une molécule \begin{equation}\mathrm{d}\overrightarrow{p}_\mathrm{molécule} = \overrightarrow{p}_\mathrm{après} - \overrightarrow{p}_\mathrm{avant} = (m\,(-\overrightarrow{u}) - m\,(\overrightarrow{u})) = -2\,m\,\overrightarrow{u}\end{equation}

Alors la paroi subit la variation de quantité de mouvement \begin{equation}\mathrm{d}\overrightarrow{p}_\mathrm{paroi} = -\mathrm{d}\overrightarrow{p}_\mathrm{molécule} = 2\,m\,\overrightarrow{u}\end{equation}

Expression de la pression cinétique : Le morceau de paroi $\mathrm{d}S$ subit donc la force due aux impacts des molécules d’expression \begin{equation}\mathrm{d}\overrightarrow{F} = \mathrm{d}N \times \dfrac{\mathrm{d}\overrightarrow{p}_\mathrm{paroi}}{\mathrm{d}t} = \dfrac{1}{6}\, n^*\,u\,2\,m\,\overrightarrow{u}\,\mathrm{d}S\end{equation} et donc une pression \begin{equation}p = \dfrac{\mathrm{d}\overrightarrow{F}}{\mathrm{d}\overrightarrow{S}} = \dfrac{1}{3}\,n^*\,m\,u^2\end{equation}

Remarques :

  • Les vecteurs $\overrightarrow{u}$ et $\mathrm{d}\overrightarrow{S}$ ayant même sens et même direction, on peut utiliser indifféremment les produits $u\,\mathrm{d}\overrightarrow{S}$ et $\overrightarrow{u}\,\mathrm{d}S$.
  • On ne confondra pas dans cette démonstration la quantité de mouvement, grandeur vectorielle $\overrightarrow{p}$, et la pression $p$.

Retour sur la loi des gaz parfaits

Avec l’expression de la vitesse quadratique moyenne, il est facile de retrouver l’équation d’état des gaz parfaits : \begin{equation}p = \dfrac{1}{3}n^*\,m\,u^2 = \dfrac{1}{3}n^*\,m\,\dfrac{3\,k_B\,T}{m} = \dfrac{N}{V}\dfrac{R}{\mathcal{N}_A}\,T \Longrightarrow p\,V = n\,R\,T\end{equation}

Energie interne

Gaz parfait monoatomique

Il est temps de parler de l’énergie interne, comme son nom l’indique il s’agit de l’énergie due aux molécules d’un gaz, pour un gaz parfait monoatomique, on ne compte que l’énergie cinétique de translation (pas d’interaction entre atomes, pas de rotation) alors \begin{equation}U = \sum_{i=1}^N \dfrac{1}{2}\,m\,v_i^2 = \dfrac{1}{2}m\,\sum_{i=1}^{N}\,v_i^2\end{equation} Or nous avons défini la vitesse quadratique moyenne comme \begin{equation}u = \sqrt{\dfrac{1}{N}\sum_{i=1}^{N}v_i^2}\end{equation} Donc \begin{equation}U = \dfrac{1}{2}m\,N\,u^2 = \dfrac{1}{2}m\,N\,\dfrac{3\,k_B\,T}{m} = \dfrac{1}{2}\,N\,\dfrac{3\,R\,T}{\mathcal{N}_A} = \dfrac{3}{2}n\,R\,T\end{equation}

Connaissant la relation entre l’énergie interne et la capacité calorifique à volume constant $U = C_V\,T$ (en considérant $C_V$ indépendante de la température), on obtient une expression simple de la capacité calorifique à volume constant et donc à pression constante :

Gaz parfait diatomique

On peut évoquer le cas des gaz parfaits diatomiques : à l’énergie cinétique de translation dont on s’est servi pour calculer l’énergie interne, on rajoute une énergie due à la rotation de la molécule. Si on assimile le facteur 3 de $\dfrac{3}{2}\,n\,R\,T$ aux degrés de liberté de translation d’un gaz parfait monoatomique, on doit rajouter deux degrés de liberté de rotation pour un gaz parfait diatomique, on obtient alors

Température cinétique

Par définition, la température cinétique est une mesure de son énergie cinétique microscopique, donc de son énergie interne.

Ressources :

Documents de référence

Derniers ajouts

Liens

Physique à l'ENSCR

physique àl'ENSCR

Retrouver, entre autres, des contenus de travaux pratiques, produits par l'équipe de physique de l'ENSCR