Questions diverses

Les intitulés des questions sont classés par ordre alphabétique.

Pour rechercher un mot dans la page, utilisez la fonction de votre navigateur
(Ctrl + F)

Fissions de l’U 235 : différentes réactions possibles ?

La distribution des produits de fission suit une courbe "en bosse de chameau". On parle aussi de courbe bimodale : elle possède deux maximums.
Il faut savoir que plus de cent nucléides différents peuvent être libérés lors de la fission de l'uranium. Toutefois, tous ces nucléides possèdent un numéro atomique entre Z=33 et Z=59.
La fission crée des noyaux de nombre de masse (nombre de nucléons) approchant A=95 (brome, krypton, zirconium) ou bien A=139 (iode, xénon, baryum). La répartition symétrique (A=118 pour l'uranium 235) des masses des produits de fission (0,1 % des fissions) et une fission en trois fragments (fission tertiaire, 0,005 %des fissions) sont très rares.

Jour sidéral, jour solaire ?

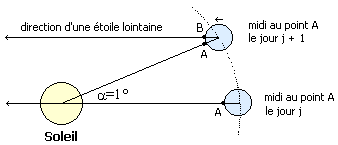
Le temps sidéral est le temps calculé selon le mouvement apparent des étoiles.

Le temps tel que nous l'utilisons est basé selon le mouvement du Soleil, le temps solaire : quand il est midi, le soleil est haut dans le ciel, et celui-ci semble tourner autour de la Terre en 24 heures.

Ceci n'est pas vrai pour le temps sidéral : si, une certaine nuit, à 23h25, vous voyez une étoile au-dessus d'une colline, la nuit prochaine on la verra au même endroit à 23h21.

Cette différence d'environ 4 minutes s'explique ainsi : en une année, la Terre effectue environ 365 tours sur elle-même par rapport au Soleil, mais effectue aussi un tour complet autour du Soleil.
Donc, par rapport aux étoiles, 365 jours solaires équivalents à 366 jours sidéraux (364 si l'orbite terrestre était rétrograde). Les jours sidéraux sont donc un peu plus courts que les jours solaires. La période réelle de l'orbite terrestre étant de 365,2564 jours solaires, la durée exacte du jour sidéral est de : 365,2564/(365,2564+1) = 0,9972697 jour solaire, soit 23h 56m 4s.

En astronomie , il existe :

• le jour sidéral : c'est la durée de la rotation de la Terre sur elle-même (environ 23 heures 56 minutes et 4 secondes )
• le jour solaire vrai : c’est l’intervalle de temps séparant deux levers , deux couchers ou deux passages du Soleil au méridien . Il varie de 23 h 59 min 39 s à 24 h 0 min 30 s , il vaut donc en moyenne 24 heures. Le jour solaire vrai est donc plus long que le jour sidéral à cause du mouvement de la Terre autour du Soleil.
• le jour solaire moyen : il dure 24 heures et commence à midi , tandis que le jour civil commence à minuit.

La durée du jour solaire varie pour plusieurs raisons :

• La vitesse angulaire de la Terre tournant autour du Soleil est plus grande quand la Terre est proche du Soleil ; ( on rappelle que la Terre décrit une ellipse autour du Soleil)
• L'angle que doit encore parcourir la Terre pour ramener le Soleil à midi n'est pas le même suivant la distance Terre-Soleil ( il est plus grand quand cette distance est petite)
• L'angle entre le plan orbite terrestre et la plan équatorial( très inclinée aux équinoxes , peu aux solstices)

Pour combler la différence de 4 minutes entre jour solaire et jour sidéral (l’année dure en moyenne 365,25, et dans notre calendrier elle dure 365 jours), on rajoute généralement un jour tous les quatre ans.
Alors cette année de 366 jours est appelée année bissextile. Ces années sont soumis à des règles :

Elles arrivent en général tous les quatre ans mais :

• Le principe général est que les années divisibles par 4 sont bissextiles, pas les autres.
• Il existe des exceptions :
  • les années divisibles par 100 ne sont pas bissextiles.
  • Exception à l'exception: les années divisibles par 400 sont bissextiles.

Avec 365,25 jours au lieu de 365,242 2 jours, il se produit un décalage des saisons (0,78 jours par siècle).
Pour serrer de plus près la réalité, on supprime trois années bissextiles séculaires (correspondant à des siècles) sur quatre : seules sont bissextiles les années séculaires dont le millésime est un multiple de 400 (1 600, 2 000, 2 400 ... ).

Finalement, on peut donc distinguer trois types d’années :

• Une année solaire = 365,2422 j solaires moyens ou année tropique
• Une année sidérale = 365,2565 j solaires moyens
• Une année calendaire : 365 ou 366 j

Masse des planètes : comment les mesure-t-on ?

On utilise la troisième loi de Kepler qui prend en compte la rotation d’objet les uns par rapport aux autres. Soit M la masse de l’objet attracteur, on a alors :

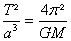
T et a sont respectivement la période et le demi-grand axe de l’orbite de l’objet qui tourne autour de l’axe attracteur.

Modérateur de la fission dans une centrale ?

Le modérateur est constitué généralement par du graphite, de l'eau lourde ou de l'eau ordinaire.

La mole et le carbone

Le carbone n'a pas toujours été l'élément de référence. Ce fut d'abord l'hydrogène (préconisé par Dalton), puis l'oxygène. Les raisons du choix des gaz en sont pratiques. Au milieu du 19ème siècle, les gaz faisaient l'objet d'importantes recherches, d'où le choix de l'hydrogène puis de l'oxygène. On s'est orienté vers le carbone, car c'est un élément fondamental depuis le 20ème siècle en chimie et de la chimie organique en particulier.

Il faut aussi noter que le carbone 12 dont il est question est un carbone « pur ». Dans la nature le carbone 12 (carbone « pur ») n'existe pas. Il est toujours associé à de petites quantités de carbone 13 et de très petites quantités de carbone 14 (ses isotopes).

Nom des couches électroniques K, L, M : quels sont leur origine ?

"La dénomination K, L, M etc...date de 1911 et elle est due à Charles Barkla (prix Nobel de physique 1917). C'est lui qui établit en 1906 la nature électromagnétique du rayonnement X en montrant qu'ils étaient polarisés transversalement. Il avait fait ses études à Liverpool, puis ses premiers travaux de recherche au Cavendish, avec 1.1. Thompson, puis fut nommé en 1913 à Edinburgh, où il resta jusqu'à sa mort en 1944.

Initialement donc, les dénominations K, L,M etc. sont relatives à des groupement de raies spectrales d'énergies voisines. La dénomination K, L, M etc. pour les niveaux d'énergie électronique est due à W. Kossel (1914), qui suggéra que si l'on extrait d'un atome un électron profond, un autre électron plus "externe" va venir combler le trou, et ainsi de suite-en cascade, avec émission de rayonnements dont la fréquence correspond aux différentes transitions. Pour passer de la vision initiale (caractérisation du rayonnement) à celle de Kossel (caractérisation des états électroniques), il fallait le modèle de Bohr de l'atome (1913), dans lequel les radiations qu'un atome peut absorber ou émettre correspondent aux transitions entre états électroniques. L'état K désigna alors l'état le plus "profond", correspondant par conséquent à la série de radiations les plus énergétiques, et ainsi de suite pour les autres états.

Mais d'où vient la lettre K ? Il me semble avoir lu quelque part, mais je ne retrouve pas la référence à l'instant, qu'elle a un rapport avec le mot allemand "Kem" qui signifie noyau. Dans une vision planétaire de l'atome, l'état K est en effet celui pour lequel le rayon carré moyen de l'orbite (calculé à partir de la fonction d'onde correspondante) est le plus petit, donc, en un certain sens, c'est l'état pour lequel un électron est le plus proche du noyau. Ce qui n'est pas tout à fait satisfaisant dans cette explication, c'est que Barkla adonné cette dénomination avant que Bohr ait peaufiné son modèle ! A partir du moment la lettre K est choisie, les autres suivent bien sûr. Sauf qu'il y eut pendant quelque temps indication qu'un autre série de raies existait, de plus haute fréquence que la série K. Elle fut donc dénommée : série J, et Barkla y fait référence dans sa conférence Nobel, en indiquant que cette série est peut-être générée dans le noyau lui-même. Comment cette question a été tranchée, et comment cette série a sombré dans les oubliettes de l'histoire, je l'ignore. .."

Nouvel an : différentes dates selon le peuple ou la religion :

• Nouvel an chinois le 29 Janvier 2006 :
  
  En Chine, la date du nouvel-an varie entre le 10 janvier et le 19 février. En 2006, le nouvel-an sera célébré le 29 janvier. A cette date commencera l'année du Chien.
  
  
• Nouvel an Musulman : 31 janvier/1er février 2006 :
  
  Le calendrier islamique est un calendrier lunaire. Il comporte 12 mois. Le 1er mois de l'année musulmane est Al-Muharram comme Janvier dans le calendrier grégorien. Le calendrier musulman a commencé le 1er de Al-Muharram de l'an 1 de l'Hégire (16 juillet 622 de l'ère chrétienne), c'est-à-dire, lorsque Mohamed a quitté La Mecque pour Médine. Hégire vient d'un mot arabe signifiant départ, exode, migration... En 2006, la fête de Nouvel an Muharram a lieu dans la nuit du 31 janvier au 1er février. Selon le calendrier musulman, nous serons en 1427.
  
  
• Nouvel an juif les 23 et 24 sept 2006 :
  
  Dans la religion juive, le nouvel an est la fête de Rosh Hashana. En 2006, elle sera célébrée les 23 et 24 septembre. Nouvelle année : 5766
  
  
• Nouvel an iranien : le 20 mars 2006 :
  
  Le nouvel an Iranien s’appelle Eid Norouz (Nowrouz : now = nouveau, rouz = jour), qui veut dire la fête du nouveau jour. L’année commence le 20 mars, le jour du printemps.
  C'est la fête la plus importante des iraniens où qu’ils soient depuis plus de 6000 ans. Elle date d'avant l'islam et le peuple iranien a pu le sauvegarder malgré les différentes invasions au cour de son histoire. Les festivités commencent le dernier Mardi de l'année qui finit, au coucher du soleil et se terminent le treizième jour de la nouvelle année qui commence.
  Pour fêter le nouvel an les enfants mettent un habit neuf et les adultes leur donnent de l’argent comme cadeau. Les gens se rendent visite. Chaque famille fait pousser sur des plateaux du blé et des lentilles pour fêter l’arrivée du printemps.
  
  
• Nouvel An bouddhiste : les 13 et 14 avril 2006 :
  
  D'après le calendrier lunaire. En Thaïlande, notamment, il s'agit d'une des fêtes les plus importantes. Les réjouissances durent 3 jours et à Chang Mai, par exemple, elles durent carrément deux semaines !
  
  
• Nouvel An russe : le 13 janvier 2006 :
  
  Les Russes enchaînent deux fêtes : le Nouvel an classique le 31 décembre, le 13 janvier, avec le Nouvel An orthodoxe (comme en Grèce ou au Moyen-Orient notamment).

Parallaxe d’une étoile : elle permet de déterminer la distance entre cette étoile et la Terre :

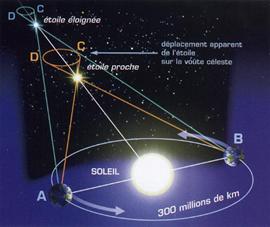
• Durant cette période, la Terre a parcouru la moitié de son orbite annuelle. Entre la première et la deuxième observation, elle se trouve de part et d'autre du Soleil et le même astre est ainsi vue sous 2 angles différents. Cet écart angulaire est, par construction, le double de la parallaxe. La connaissance de cette parallaxe, ajoutée à celle de la mesure de la distance Terre-Soleil, donne immédiatement (à l'aide d'une formule trigonométrique, voir "Applications") la distance entre l'astre et la Terre.
  
  
• On peut utiliser une méthode spectrophotométrique en mesurant la magnitude apparente (luminosité vue depuis la terre) et la magnitude absolue (luminosité à une distance de 10 parsecs).
  
  

Qu'est-ce que le parsec ?

Le parsec (symbole pc) est une unité de longueur utilisée en astronomie. Son nom vient de la contraction de « parallaxe-seconde ».

Il est défini comme étant la distance à laquelle une unité astronomique (ua) sous-tend un angle d'une seconde d'arc.

Rayons atomiques : comment les mesure-t-on ?

La diffraction des rayons X est utilisée pour déterminer les informations structurelles de matériaux à l'échelle atomique (réseau cristallin), nanométrique (molécules) et jusqu'au micromètre (comme dans le cas de films minces) de liquides, de poudres, de films en couches et de cristaux parfaits.

Qu'est-ce que le speckle laser ?

• Le Speckle ou granularité Laser s'observe à chaque fois qu'un objet diffusant est éclairé par une source cohérente (ex : Laser). Cet effet indésirable en holographie ou en astronomie peut être très utile dans d'autres domaines (ex : traitement d'image, mesure de déplacement, rotation, déformation, vibration, rugosité, vitesse, etc…).
  
  
• Le speckle est une conséquence de la cohérence spatiale du faisceau laser : lorsqu’un laser éclaire une surface diffusante, les ondes émises par les diffuseurs s’ajoutent en amplitude, et non en intensité comme c’est le cas avec une source classique. On observe alors des interférences, bien que le milieu diffusant soit désordonné.
  
  
• Expérimentalement :
  pour observer un speckle de grande taille, placez après le laser une lentille de courte focale (ou un objectif de microscope pas trop puissant) suivie d’un écran diffusant (calque). Observez la lumière diffusée sur un écran éloigné, à la distance D du diffuseur (Sextant 206). On observe des grains de speckle dont la taille L ne dépend pas de la nature du diffuseur, mais uniquement de la largeur w du faisceau dans le plan du diffuseur (L = 2(lambda)D/w : diffraction de Fraunhofer).
  
  
• Nettoyage de faisceau :
  Le speckle est souvent gênant. On peut l’éliminer en procédant à un « nettoyage de faisceau » à l’aide d’un objectif de courte focale suivi d’un diaphragme de très petite dimension (quelques 10 µm) centré sur le foyer de l’objectif.
  En effet, dans le plan focal de l’objectif, le profil d’intensité est donné par la diffraction de Fraunhofer. C’est donc la transformée de Fourier du profil d’intensité du faisceau avant l’objectif. Le faisceau gaussien « propre » se retrouve au centre de la figure de diffraction (la TF d’une gaussienne est une gaussienne, de petite dimension si l’objectif est puissant), alors que le speckle, qui correspond à des fluctuations de haute fréquence spatiale, se retrouve au bord de la figure de diffraction. Il sera donc filtré par le diaphragme (qu’on appelle pour cette raison le « filtre spatial ») si celui-ci est bien centré et si sa dimension est assez faible (il doit être juste assez grand pour laisser passer le faisceau gaussien « propre », sa taille optimale dépend donc à la fois du waist du laser et de la focale de l’objectif utilisé).
  Ce montage est délicat à réaliser car il nécessite du matériel de précision (type Microcontrôle) et un support stable.
  
  

Système heures-minutes-secondes : d’où vient-il ?

• Une journée, une heure, une semaine... :
  
  Très tôt la journée a été organisée en différentes périodes. Chez les Babyloniens (il y a 4000 à 5000 ans) le jour était divisé en 6 périodes ou veilles : trois du lever du soleil à son coucher et trois autres du coucher au lever (6 est un nombre parfait car la somme de ses diviseurs est égale à son double : 12 = 1 + 2 + 3 + 6). Bien entendu selon les saisons ces six périodes n'avaient pas la même durée. Ensuite on affina ces périodes en les raccourcissant : on passa à six veilles de jour et six de nuit. Cela faisait 12 périodes toujours de longueurs inégales suivant les saisons.
  L'Egypte ancienne adopta également ce système.
  Cependant les astronomes d'alors étaient soucieux de plus d'exactitude dans leurs calculs prévisionnels et divisèrent encore par deux les unités de temps.C'est ainsi que nos journées furent découpées en 24 unités de temps.
  La notion d'heure (vient du latin hora) existe depuis des millénaires, mais elle ne correspondait pas à la notion actuelle : chez les grecs elle correspondait à toute division du temps annuelle saisonnière puis horaire... La notion de semaine (septimana : groupe de 7 jours) est aujourd'hui en usage chez presque toutes les nations civilisées. Sa durée de 7 jours semble s'apparenter aux phases de la Lune (7 jours pour passer de la nouvelle lune à son premier quartier...) . Elle a peut-être aussi son origine dans les sept planètes que les Babyloniens croyaient connaître : Saturne, Jupiter, mars, le Soleil, Vénus, Mercure, la Lune. On a depuis éliminé la Lune (satellite de la Terre), le Soleil (étoile) mais nous connaissons maintenant Uranus, Neptune Pluton. Son emploi n'était pas universel chez tous les anciens. Les Egyptiens, les Chinois et les Grecs comptèrent d'abord par décades. Les Hébreux furent les premiers à l'utiliser. Chez les Babyloniens le nombre 7 était considéré comme néfaste d'où l'origine du repos hebdomadaire (CF Le calendrier Que sais-je ?). La semaine pénétra tardivement en Grèce et chez les Alexandrins. Son emploi en Occident date seulement du IIIe siècle de notre ère : les calendriers antérieurs n'en font pas mention.
  Pour le plan divin et la création du monde en 6 jours suivi d'un repos le septième... notons seulement que les musulmans se reposent le vendredi, les israélites le samedi et les chrétiens le dimanche.
  Remarques :
  Lundi vient de Lunae dies, jour de la Lune ;
  Mardi vient de Martis dies, jour de Mars ;
  Mercredi jour de Mercure ;
  Jeudi, c'est Jovi dies, jour de Jupiter ;
  Vendredi, c'est Veneris dies, jour de Vénus ;
  Samedi, c'est Sabbati dies, jour du Sabbat ou en anglais Saturday, jour de Saturne ;
  Dimanche, c'est Dominica dies, jour du Seigneur substitué au Soleil par les chrétiens mais en anglais et en allemand on trouve Sunday et Sonntag : jour du Soleil.
  
  
• Pourquoi pas 10 ?
  
  Pourquoi avoir divisé une journée entière par 6 au départ et non pas par 10 ? Parce que le système nous vient des Babyloniens justement. Ce système nous a été transmis par les Grecs et les Romains. Les astronomes de Babylone n'utilisaient pas notre système décimal, ils comptaient dans un système de numération de position de base 60 : ils comptaient de 60 en 60 (60 est très commode car il admet beaucoup de diviseurs).
  L'année cyclique correspondait à un cercle de 360° (360 jours) et ce cercle était divisé en six parties de 60° : toujours de 60 en 60.
  Le cercle a aussi figuré une journée entière puisqu'elle correspondait à un "cycle"du soleil. Elle aussi a été divisée en six : trois sections de jour et trois sections de nuit vues ci-dessus. Ces sections ont donc été divisées plusieurs fois par deux pour obtenir une plus grande précision avec le découpage en 24 heures.
  De la même façon, une heure a été divisée en 60 minutes. Remarquons que l'appellation est la même pour les angles : 1 degré est constitué de 60 minutes, ainsi un angle de 1,5° correspond à 1° plus la moitié de 60° donc à 1° et 30 minutes.
  Minute vient du latin minuta signifiant menu (petit).
  
  
• Une heure de 60 minutes :
  
  De la même façon, une heure a été divisée en 60 minutes. Remarquons que l'appellation est la même pour les angles : 1 degré est constitué de 60 minutes, ainsi un angle de 1,5° correspond à 1° plus la moitié de 60° donc à 1° et 30 minutes. Cependant nous avons eu besoin de plus en plus de précision surtout au cours du XXe siècle et la minute s'est elle aussi retrouvée divisée en 60 parties appelées secondes (pour seconde division de l'heure). La seconde est elle -même divisée en 60 parties appelées tierces.
  Depuis 1967, la seconde atomique a été définie en fonction d'une durée de radiation atomique.
  Elle a été encore divisée mais cette fois on a utilisé le système décimal. On parle alors de dixièmes de seconde, de centièmes de seconde et de millièmes de seconde. Avec les gros ordinateurs, on va beaucoup plus loin en utilisant des milliardièmes de seconde (nanoseconde) et cela continue... puisqu'on est capable de mesurer la durée de certaines opérations de notre cerveau.
  
  
• Le bâton d’Ishango :
  
  L'origine des mathématiques ? La Grèce antique ou l’Égypte, pense-t-on d'emblée. ERREUR ! Car un petit bout d'os d'une dizaine de cm de long et jalousement dissimulé dans les collections du Muséum des sciences naturelles de Belgique vient bousculer cette belle assurance.
  L'os d'Ishango, encore appelé le "bâton d'Ishango", du nom de la région d'Afrique centrale (près du lac Edouard, en bordure de l'ex-Congo belge) où il a été découvert voici plus de 50 ans par un archéologue du Plat Pays, apparaît comme la plus antique des machines à calculer. Une machine vieille de 20 000 ans ! C'est l'analyse des séries de traits gravés sur les diverses faces de ce petit os qui jette le trouble. Réunis en différents ensembles, on peut aisément y identifier plusieurs relations mathématiques : une suite de nombres premiers (11, 13, 17, 19) dans la première colonne par exemple, des séries de duplications (3 et 6, 4 et 8 ou encore 5 et 10). Mais surtout, les ethno-mathématiciens détectent dans ces groupements des systèmes arithmétiques de base 12. Une découverte indiscutable.
  Bien que nous utilisions surtout aujourd'hui le système décimal (de base 10), le système duodécimal ne nous est pas inconnu. Il suffit de penser au nombre de mois dans l'année... ou d'heures dans une journée (12 dans les deux cas). Le bâton d'Ishango, vieux de 200 siècles, est bel et bien le plus ancien objet témoignant d'une conscience mathématique chez nos lointains ancêtres. Et, depuis la semaine dernière, cet étonnant artefact est désormais visible par tous. Cette calculette millénaire a enfin quitté les sombres réserves de l'Institut des sciences naturelles de Belgique pour être exposé dans la salle la plus prestigieuse du Muséum : celle des origines de l'homme. Une occasion unique de renouer avec les mathématiques.
  
  

Vitesse de la lumière : comment la mesure-t-on actuellement ?

Différentes mesures ont été données pendant ces dernières années. En 1849, Fizeau découvrit une valeur de 315 300 km /s grâce à l'utilisation d'un système de roue dentée. Cette roue dentée était en rotation. Une source lumineuse envoyait la lumière. Cette lumière passait entre deux dents de la roue et elle se réfléchissait sur un miroir blanc et refaisait en arrière le même trajet. Normalement, si la vitesse était correcte elle devait se réfléchir et aller frapper les dents suivantes pour aller une nouvelle fois se réfléchir sur le miroir. Donc l'observateur ne pouvait pas voir le rayon réfléchi. A son époque Fizeau prit une roue qui avait 500 dents et lui donna une vitesse de rotation de 18 tours par seconde. La distance du trajet entre la roue et le miroir était de 17 km.
C'est en 1973, l'utilisation d'un laser à gaz a permis de mesurer la valeur actuelle de 299.792.458 m/s à 1,2 m/s près.