Licence 1 > Mécanique 1 > Cours 2 : chutes avec frottements nouvelle version

M12 : chutes avec frottements

Ce chapitre est disponible intégralement en vidéos. La playlist dédiée est disponible ici. La première vidéo peut être visionnée ci-dessous :

Vous pouvez également visionner le chapitre séquence par séquence :

Cette version est une version actualisée du cours, nous étudiions précédemment la chute d'un parachutiste (retrouver la vieille version du cours ici), nous avons décidé de faire un étude expérimentale "en direct" avec les étudiants en traitant le cas de la chute du volant de Badminton.

Introduction

Nous avons modélisé au chapitre précédent le corps qui chute dans le champ de pesanteur en considérant que les frottements de l'air étaient négligeables. Cette supposition n'ayant qu'une utilité théorique, nous complexifions ici notre modèle en tenant compte de ces frottements : comment ceux-ci vont modifier la trajectoire du corps qui chute?
Ce sera l'occasion de voir que ces frottements peuvent être de deux types, linéaires ou quadratiques, nous allons alors rencontrer deux types d'équations différentielles : la résolution de la première ne nous posera pas de problème ; mais la résolution de la seconde est moins aisée. Nous en profiterons pour voir une méthode numérique itérative permettant d'approcher la forme de la solution : la méthode d'Euler.
Enfin parmi les deux modèles de forces de frottement, lequel se révèle le plus juste pour étudier la chute d'un volant de badminton ? Nous essaierons d'y répondre en confrontant expérience et théories.

Problème 3

On lâche sans vitesse initiale un volant de badminton (de masse 6 g) d'une hauteur de 2 m environ. Quel est son mouvement ? Peut-on par l'expérience, trouver le type de frottement qui s'exerce sur ce volant?

Etude expérimentale

Le principe est classique, après avoir enregistré une vidéo de chute du volant, on l'exploite avec un logiciel permettant d'effectuer une chronophotographie:

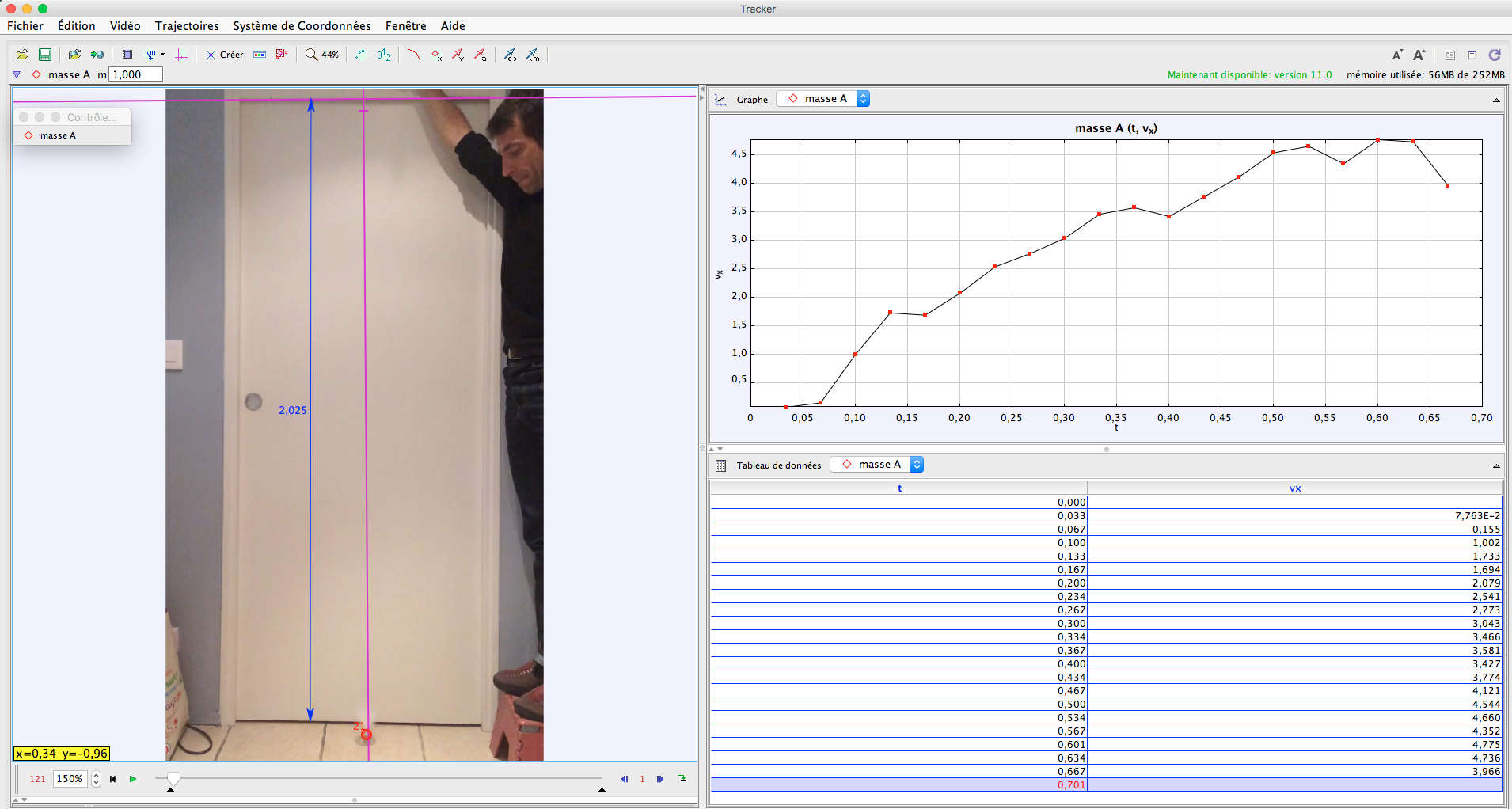
On en retire la position et la vitesse du volant en fonction du temps (d'autres données sont également exploitables avec le logiciel utilisé ici, nommé Tracker (macOS)).

Le but est à présent d'étudier théoriquement notre problème avec les deux types de frottement possibles, et de voir quel modèle colle le plus à la réalité.

Système

Le volant de Badminton considéré ponctuel.

Référentiel et base

On étudie son mouvement dans un référentiel terrestre lié au sol, ce référentiel est considéré galiléen pendant la durée de la chute. On utilisera une base cartésienne à une dimension pour suivre l'évolution du volant : un axe O$z$ vertical descendant avec origine au point de lâcher constituera la base d'étude.

On considère en effet que le mouvement du volant est strictement vertical.

Forces

Bilan des forces

Le volant est soumis à son poids noté $\overrightarrow{P}$, force à distance exercée par la Terre sur lui. On rappelle que le poids est égal à la force de gravitation qui s'exerce entre la Terre et le volant.
Il est soumis aux forces de frottements de l'air, modélisées par une force de contact notée $\overrightarrow{f}$. Cette force peut aussi être nommée résistance de l'air.

Deux types de forces de frottements

La force de frottements de l’air peut prendre deux formes :

Frottements linéaires

Dans le cas d’une vitesse faible, la force de frottement est proportionnelle à la vitesse :

\begin{equation}\overrightarrow{f} = -h\,\overrightarrow{v}\end{equation}

On parle de frottements linéaires. $h$ est une constante qui dépend de la nature du fluide et des caractéristiques de l’objet. Par exemple pour une sphère de rayon $r$, on a $h = 6\,\pi\,\eta\,r$ où $\eta$ est la viscosité du fluide.

Frottements quadratiques

Dans le cas d’une vitesse importante, la force de frottement est proportionnelle au carré de la vitesse :

\begin{equation}\overrightarrow{f} = -h'\,v\,\overrightarrow{v}\end{equation}

On parle de frottements quadratiques. $h'$ est aussi une constante qui dépend du fluide et des caractéristiques de l’objet mais elle prend une autre forme que par rapport à $h$ : son expression est du type $k' = \frac{1}{2}\,\rho\,C_x\,S$ avec $\rho$ la masse volumique du fluide, $S$ la surface frontale de l’objet et $C_x$ le coefficient de trainée qui dépend de la géométrie du corps. Par exemple, voici trois géométries et trois valeurs de $C_x$ :

Valeur du $C_\mathrm{x}$ en fonction de la géométrie du corps

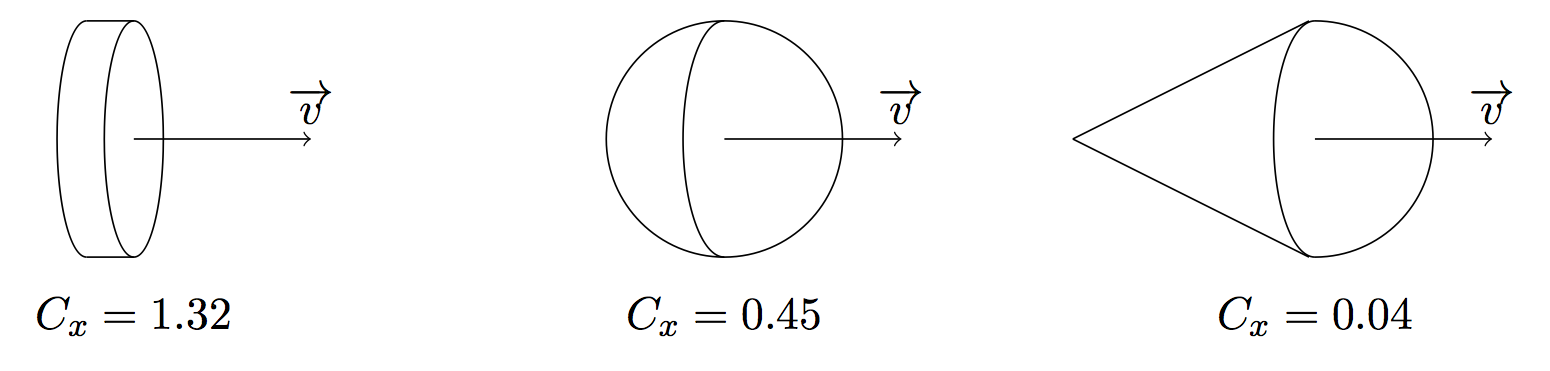
Ce coefficient de trainée peut se calculer pour une sphère lisse (sans rugosité) dans le cas d'écoulement à faible vitesse (à faible nombre de Reynolds), il dépend alors du nombre de Reynolds.

Pour des écoulements turbulents (à grand nombre de Reynolds $> 10^3$), on mesure le $C_\mathrm{x}$ en soufflerie. En sachant qu'il est constant pour un corps donné.

Utilisation de la 2^ème loi de Newton

\begin{equation}\sum \overrightarrow{F} = m\,\overrightarrow{a} \Longleftrightarrow \overrightarrow{P} + \overrightarrow{f} = m\,\overrightarrow{a}\end{equation}

Résolution du problème dans le cas de frottements linéaires

Equation différentielle

Le PFD donne : $m\,\overrightarrow{g} - h\,\overrightarrow{v}= m\,\overrightarrow{a}$.

On projette maintenant cette relation sur l’axe Oz vertical descendant.

\begin{equation}\begin{aligned} m\,g - k\,v_z = m\,a &\Longleftrightarrow m\,\dfrac{\mathrm{d}v_z}{\mathrm{d}t} + k\,v_z = m\,g \\ &\Longleftrightarrow \boxed{\dfrac{\mathrm{d}v_z}{\mathrm{d}t} + \dfrac{k}{m}\,v_z = g} \end{aligned}\end{equation}

On obtient donc une équation différentielle en $v_z$, linéaire du premier ordre à coefficients constants. On sait résoudre cette équation mathématiquement. Une fois l’expression de la vitesse $v_z$ obtenue, on en déduira la position par intégration.

Une notation particulière

Souvent ce type d’équation sera écrite ainsi :

\begin{equation}\dfrac{\mathrm{d}v_z}{\mathrm{d}t} + \dfrac{v_z}{\tau} = -g \quad \text{ avec } \quad \tau = \dfrac{m}{h}\end{equation}

La notation $\tau$ fait référence à un temps. En effet, la grandeur $\tau = \dfrac{m}{h}$ est un temps caractéristique de la fonction $v=f(t)$, comme nous allons le voir par la suite.

Solution de l’équation différentielle

Principe

Une équation différentielle linéaire avec second membre se résout en deux temps :

On cherche d’abord la solution $s_h$ de l’équation homogène, c’est à dire l’équation sans second membre ;
On cherche une solution particulière $s_p$, c’est à dire une solution qui a même forme que le second membre (si le second membre est constant, la solution particulière recherchée sera une constante).

La solution de l’équation différentielle avec second membre est la somme de la solution homogène et de la solution particulière : $s = s_h + s_p$.

Attention, dans la solution de l’équation homogène apparaissent souvent des constantes (une si l’équation est du premier ordre, deux si elle est du deuxième ordre). La détermination de ces constantes à l’aide des conditions initiales doit être menée en tenant compte de la solution particulière.

Pour notre problème

On recherche la solution de l’équation complète , qui est une vitesse.

Solution de l’équation homogène

Equation homogène : $\dfrac{\mathrm{d}v}{\mathrm{d}t}+\dfrac{v}{\tau} = 0 \quad$ $\Longrightarrow $ Solution : $v_h = A\,e^{\left(-\dfrac{t}{\tau}\right)}$ avec $A$ une constante.

On peut vérifier en dérivant une fois $v_h$ que cette solution vérifie l’équation homogène.

Solution particulière

Le second membre étant constant (égal à $g$), on cherche une solution particulière $v_p = \mathrm{cste}$. Alors $\dfrac{\mathrm{d}v_p}{\mathrm{d}t} = 0$ et on obtient $v_p = g\,\tau$.

Solution globale

On a donc :

\begin{equation}v_z = A\, e^{\left(-\dfrac{t}{\tau}\right)} + g\,\tau\end{equation}

On peut maintenant déterminer $A$ à l’aide des conditions initiales :

\begin{equation}\text{A }t=0 \text{ : } v(t=0) = 0 = A + g\,\tau \Longleftrightarrow A = -g\,\tau\end{equation}

Et finalement :

\begin{equation}v_z = g\,\tau\, \left( 1-e^{\left(-\dfrac{t}{\tau}\right)}\right)\end{equation}

Courbe $|v_z|=f(t)$ et caractéristiques

Courbe

On souhaite visualiser la norme de la vitesse en fonction du temps. Son expression est donc :

\begin{equation}v_z = g\,\tau \left(1 - e^{\left(-\dfrac{t}{\tau}\right)}\right)\end{equation}

Voici la courbe obtenue :

Vitesse du volant de badminton dans le cas de frottements linéaires

La vitesse augmente d’abord fortement, puis de plus en plus faiblement pour atteindre une valeur limite.

Vitesse limite

La valeur de la vitesse limite peut être obtenue en calculant la limite de $v_z(t)$ quand le temps tend vers l’infini:
\begin{equation}\lim_{t\rightarrow \infty} v_z(t) = \lim_{t\rightarrow \infty} g\,\tau \left(1 - e^{\left(-\dfrac{t}{\tau}\right)}\right) = g\,\tau\end{equation}
On peut également la trouver à partir de l’équation différentielle . En effet, la vitesse limite est constante, on a ainsi :
\begin{equation}\begin{aligned} \dfrac{\mathrm{d}v_{z\,\mathrm{lim}}}{\mathrm{d}t} + \dfrac{v_{z\,\mathrm{lim}}}{\tau} = g \Longleftrightarrow 0 + \dfrac{v_{z\,\mathrm{lim}}}{\tau} = g \\ \Longleftrightarrow v_{z\,\mathrm{lim}} = g\,\tau \\ \Longleftrightarrow \boxed{v_{z\,\mathrm{lim}} = g\,\tau}\end{aligned}\end{equation}

Temps caractéristique

La grandeur $\tau = \dfrac{m}{h}$ est caractéristique de l’évolution de la vitesse dans le temps. Dans ce type d’évolution, on parle de régime transitoire et de régime permanent :

le régime est transitoire tant que la vitesse évolue;
le régime est permanent lorsque la vitesse limite est atteinte.

Le temps $\tau$ est un bon indicateur pour savoir quand on passe d’un régime à l’autre : on considère qu’au bout de $5\tau$, le régime permanent est atteint.

Détermination de $\tau$

On peut obtenir la valeur de $\tau$ graphiquement : on cherche l’abscisse du point d’intersection entre la tangente à la courbe en $t=0$ et l’asymptote quand $t \rightarrow \infty$ de la courbe $|v_z|=f(t)$.On obtient ainsi la limite entre régime transitoire et régime permanent :

Différents régimes lors de la chute avec frottements

Obtention de la position

La fonction $z=f(t)$ s’obtient en intégrant la fonction $v_z=f(t)$ :

\begin{equation}\begin{aligned} & v_z = g\,\tau \left(1-\exp\left(-\dfrac{t}{\tau}\right)\right) = g\,\tau - g\,\tau\,\exp \left(-\dfrac{t}{\tau}\right) \\ \Longrightarrow & z(t) = g\,\tau\,t+g\,\tau^2\,\exp \left(-\dfrac{t}{\tau}\right) + \mathrm{cste} \end{aligned}\end{equation}

La constante est obtenue à l’aide de la condition initiale de position :
A $t=0$, $z=h$ donc $g\,\tau^2 + \mathrm{cste} = 0 \Longleftrightarrow \mathrm{cste} = - g\,\tau^2$

On a finalement :

\begin{equation}\boxed{z(t) = g\,\tau\,t + g\,\tau^2 \left(\exp \left(-\dfrac{t}{\tau}\right)-1\right)} \end{equation}

On prend comme altitude de départ $h = 4000\,\mathrm{m}$.

Position en fonction du temps dans le cas de frottements linéaires