Licence 1 > Optique 1 > Cours 1 : lois de l'optique géométrique
O1 : lois de l'optique géométrique
Introduction
Dans ce premier cours d’optique, après un retour historique sur le concept de la lumière, on rappellera des généralités concernant celle-ci avant de s’intéresser à proprement parlé aux lois de l’optique géométrique comme la propagation rectiligne, le principe de Fermat ou les lois de la réfraction.
Rappelons que les connaissances en optique ont permis de corriger la vue, de permettre la photographie (que ce soit argentique ou numérique), de construire les instruments d’optique permettant de sonder l’univers mais aussi de faire fonctionner un lecteur cd ou dvd, d’amener internet par fibre optique dans les foyers ...
Histoire de l’optique géométrique
Les anciens, la lumière, la vision
Parmi les anciens scientifiques trois théories s’affrontaient :
Les atomistes pensaient que la vision d’un objet était due à l’arrivée dans notre oeil d’une réplique de celui-ci. Ainsi chaque objet émet en permanence des simulacres de lui-même qui tombent ou non dans l’oeil de l’observateur pour communiquer sa forme. Dans ces idées, il n’existe donc pas de lumière ;
De leur côté les pythagoriciens pensaient que l’oeil émettait en ligne droite des rayons venus du feu intérieur de chaque individu et permettaient de voir les objets. Ainsi les chats avaient un feu intérieur plus intense que les hommes puisqu’ils pouvaient voir la nuit.
Euclide (-300 av JC) fait partie de ces scientifiques, il a aussi décrit dans un ouvrage l’obtention d’ombres, la réflexion sur miroirs et la réfraction. Son optique est géométrique.
Enfin Aristote s’oppose à l’idée que l’oeil émet la lumière, pour la plus simple des raisons : si l’oeil émettait la lumière, nous pourrions voir la nuit aussi bien que le jour. Il pense plutôt que la sensation de vision est causée par une propagation de l’objet vers l’oeil. Malheureusement pour lui, dans ce domaine il ne sera pas écouté.
Le fondateur de l’optique
ALHAZEN est le plus grand physicien arabe du moyen-âge et peut être considéré comme le fondateur de l’optique.
Selon lui la lumière a une existence indépendante de l’objet vu ou de l’oeil, elle est émise par une source principale auto-lumineuse qui émet de la lumière se propageant en ligne droite. Il évoque même la diffusion de la lumière (un grain de poussière peut devenir source accidentelle de lumière).
Il explique la réflexion de la lumière (par analogie mécanique), la réfraction par changement de vitesse de la lumière à l'interface entre deux milieux.
L’optique en occident au moyen-âge
On commence dés le XIIIème siècle à utiliser des verres convexes pour corriger la vue. Au cours de ce même siècle, un dénommé De Freiberg sera le premier scientifique à donner une explication de l’arc-en-ciel en parlant de réflexion et de réfraction dans la goutte d’eau.Il pense que la lumière est fait d’éclat et d’obscurité et qu’un mélange savant de ces deux substances permet d’obtenir toutes les couleurs.
La contribution des illustres
Kepler (XVIIème) introduit la notion d’image virtuelle, explique la formation de l’image sur la rétine et comment on corrige la vue avec des lentilles.
Snell et Descartes sont les pères des lois de la réfraction. Le premier établit les lois expérimentalement alors que le deuxième les explorent théoriquement avec notamment des histoires de vitesses (erronées) : "la lumière court plus vite dans les milieux les plus denses" ...
Pierre de Fermat rejette l’explication de Descartes pour la réfraction, car il lui semble absurde que la lumière se propage plus rapidement dans un milieu plus dense. Il suppose le contraire et réussit à démontrer la loi de Snell en invoquant le principe du moindre temps : la lumière se propage entre deux points de manière à minimiser le temps de parcours entre ces deux points.
Mais ces considérations gênent les cartésiens : Comment la lumière peut-elle connaître son point d’arrivée à l’avance pour ainsi calculer le chemin qui minimise le temps requis ?
Fermat a raison, son principe peut être démontré à l’aide de la théorie ondulatoire.
Newton expliquera la dispersion de la lumière à l’aide de sa fameuse expérience à deux prismes, il prouvera ainsi que la lumière blanche est un mélange de plusieurs couleurs. Cette dispersion avait été observée au préalable par De Freiberg qui pensait déjà que les couleurs étaient une propriété inhérente à la lumière. Contrairement à Descartes qui pensait que c’était la surface du milieu réfringent qui donnait sa couleur à la lumière.
Quelques généralités sur la lumière
Nature de la lumière
Le problème historique
Dans notre retour historique sur la lumière, nous nous sommes arrêté à Newton. Ce grand scientifique n’a pas seulement expliqué la dispersion de la lumière mais avait un avis sur sa nature : il prône un modèle corpusculaire de la lumière par analogie mécanique, la lumière rebondit sur des objets opaques.
A contrario, un dénommé Huygens, à la même époque, décrit la lumière comme une onde qui se propage comme les ondes à la surface de l’eau. Un peu plus tard (début XIXème), Fresnel renforce l’idée d’une onde de lumière en expliquant les phénomènes de diffraction et d’interférences. Puis Maxwell établit que la lumière est une onde électromagnétique de fréquence particulière.
Le modèle corpusculaire de Newton semble définitivement obsolète lorsque Hertz (fin XIXème) découvre l’effet photoélectrique (arrachement d’électrons d’un métal recevant un faisceau lumineux). Einstein reprend alors l’idée de Newton en postulant l’existence de grains de lumière appelés photons.
Sa vrai nature
Ainsi la lumière n’est ni une onde, ni un ensemble de particules mais une onde-particule (l’ornithorynque n’est ni un canard, ni un castor mais un ornithorynque).
Pour notre étude
Dans ce cours d’optique, on retiendra que la lumière est une onde électromagnétique, c’est à dire un champ magnétique et un champ électrique variables qui se propagent.
Propriétés de la lumière, propagation dans un milieu
Fréquence, période, longueur d’onde
Une lumière monochromatique (d’une seule couleur) peut être caractérisée par trois nombres :
Sa fréquence \(\nu\) ("nu") exprimée en Hertz (Hz), qui est la fréquence de variation du champ électrique ;
Sa période \(T\) exprimée en seconde (s), on a : \(\boxed{T=\dfrac{1}{\nu}}\) ;
Sa longueur d’onde \(\lambda\) exprimée en mètre (m), on a \(\boxed{\lambda = \dfrac{c}{\nu}}\) où \(c\) est la célérité de la lumière dans le vide.
La lumière telle qu’on l’entend, c’est à dire visible, s’étend sur des longueurs d’ondes allant de 380 (violet) à 780 (rouge) nanomètre (\(\mathrm{nm}\)) environ.
Dans le spectre électromagnétique, elle ne représente qu’une toute petite gamme de fréquences :

Attention, la grandeur physique qui caractérise une onde lumineuse (une couleur) est la fréquence : en effet, plus loin, nous verrons que la vitesse de propagation de la lumière n’est pas toujours égale à \(c\) et donc la longueur d’onde changera selon cette vitesse de propagation.
Mais généralement, on caractérise une couleur par sa longueur d’onde dans le vide.
Vitesse de propagation
L’onde électromagnétique, donc la lumière, se propage dans le vide à la vitesse \(c = 3,00 \times 10^8 \mathrm{m.s^{-1}}\) .
La mesure expérimentale de c la plus connue est celle réalisée par Fizeau fin XIXème à l’aide de deux miroirs et d’une roue dentée.
Dans les autres milieux, elle se propage moins vite. Ceci est caractérisé par l’indice de réfraction d’un milieu.
Indice de réfraction d’un milieu
Il est obtenu par le rapport entre la célérité de la lumière dans le vide et la vitesse à laquelle elle se propage dans le milieu considéré :
\begin{equation}\boxed{n = \dfrac{c}{v}}\end{equation}
avec \(v\) exprimé en \(\mathrm{m.s^{-1}}\).
Ainsi l’indice le plus petit qui existe est 1 et n > 1.
Voici quelques valeurs :
| Vide | 1 |
| Eau | 1.3 |
| Verre | 1.5 |
| Diamant | 2.42 |
Attention, cet indice de réfraction dépend de la couleur de la lumière (voir ci-dessous), on prend généralement comme référence la couleur jaune du doublet du sodium.
Dispersion de la lumière, milieux dispersifs
Il n’y a pas que la nature du milieu qui influe sur la vitesse de propagation de la lumière, mais sa fréquence (sa couleur) aussi.
En effet, l’indice optique d’un milieu dépend de la fréquence de la vibration qui s’y propage, un tel milieu est appelé milieu dispersif.
Ainsi l’eau est un milieu dispersif ce qui permet l’observation d’arc-en-ciel.
Exemple de milieu transparent dispersif Le verre est un milieu dispersif pour les ondes lumineuses puisque le bleu (de grande fréquence) se propage moins vite que le rouge (de petite fréquence). L’indice du verre pour le bleu est plus grand que l’indice du verre pour le rouge.
Exemple de milieu non dispersif L’air n’est pas un milieu dispersif pour les ondes sonores puisque toutes les fréquences se propagent à la même vitesse (environ \(340\;\mathrm{m.s^{-1}}\)).
Milieu et longueur d’onde
Si on transpose la définition de la longueur d’onde d’une radiation dans le vide à un milieu dispersif, on voit que cette longueur d’onde dépend du milieu :
\begin{equation}\boxed{\lambda_{\text{milieu}} = v\times T = \dfrac{c}{n} \times T = \dfrac{\lambda_{\text{vide}}}{n}}\end{equation}
Les longueurs d’ondes dans un milieu sont comprimés.
A retenir
Plus la fréquence de la vibration est grande (plus sa longueur d’onde est petite), plus la vitesse de propagation est faible, plus l’indice du milieu est grand.
Loi de Cauchy
Pour la propagation de la lumière visible dans le verre, cette loi donne l’évolution de l’indice d’un verre en fonction de la longueur d’onde :
\begin{equation}\boxed{n(\lambda) = A + \dfrac{B}{\lambda^2}}\end{equation}
avec A et B des constantes positives qui dépendent du milieu, $\lambda$ la longueur d'onde dans le vide de la radiation.
Application : quels sont les ordres de grandeurs de A et de B, sachant que l’indice varie peu avec la longueur d’onde (variation de l’ordre de \(1\times 10^{-2}\)) ?
L’indice d’un milieu est de l’ordre de l’unité, donc A est du même ordre de grandeur. Le rapport \(\dfrac{B}{\lambda^2}\) doit être de l’ordre de \(1\times 10^{-2}\), donc B de l’ordre de \(1\times 10^{-2} \times (500\times 10^{-9})^2 \simeq \times 10^{-15}\) (\( 500\times 10^{-9} = 500 \mathrm{nm}\), longueur d’onde moyenne des ondes lumineuses visibles).
Le modèle du rayon lumineux
Isoler un rayon ?
Soit un faisceau lumineux issu d’une lampe torche par exemple : peut-on isoler un rayon lumineux ? Par quel moyen ? Que se passe-t-il ?
Il est en effet pas possible d’isoler un rayon d’un faisceau en utilisant par exemple un trou de petite taille car à partir d’une certaine limite de taille du trou, le faisceau n’est pas rétréci mais au contraire s’étale. La lumière s’étalera d’ailleurs d’autant plus que le trou sera petit : c’est la diffraction. Celle-ci a été découvert par Grimaldi au XVIIème siècle en faisant l’expérience bien connue de la diffraction de la lumière par un cheveu.
A retenir
Ainsi, l’approximation de l’optique géométrique et le modèle du rayon lumineux sont valables lorsque la longueur d’onde de la lumière est petite devant les dimensions des obstacles et ouvertures qu’elle rencontre.
Rayons lumineux et nature ondulatoire de la lumière
La lumière est une onde électromagnétique qui se propage à la célérité c : on appelle surface d’onde l’ensemble des points pour lesquels le champ électrique de l’onde lumineuse à la même valeur à un instant t.
A retenir
L’énergie lumineuse se propage suivant des trajectoires perpendiculaires en tout point aux surfaces d’onde, chaque trajectoire est appelé rayon lumineux.
Lois de l’optique géométrique
Milieu de propagation
Dans tout ce qui va suivre, on se place dans le cas où le milieu de propagation est homogène et isotrope :
Homogène : les propriétés physiques (densité, indice de réfraction, ...) sont les mêmes en tout point du milieu. Exemple de milieu non homogène : l’air situé juste au dessus d’une route, cette non homogénéité donne naissance aux mirages.
Isotrope : ces propriétés physiques sont identiques dans toutes les directions de propagation du rayon lumineux. Exemple de milieu non isotrope : le cristal de quartz, la vitesse de propagation du rayon lumineux n’est pas la même dans toutes les directions. S’il existe deux directions avec deux vitesses différentes, on parle de matériaux biréfringents (deux indices optiques selon deux directions).
Trois lois fondamentales
Propagation rectiligne
A retenir
Dans un milieu homogène et isotrope, les rayons lumineux sont des droites.
On peut remarquer qu’il s’agit du plus court chemin pour aller d’un point à un autre.
La géométrie nous permettra donc de construire le trajet de la lumière d’où le nom d’optique géométrique.
Retour inverse de la lumière
A retenir
Que la lumière se propage de A vers B ou de B vers A, elle emprunte la même trajectoire (A et B sont sur le même rayon lumineux).
Indépendance des rayons lumineux
A retenir
Il n’y a pas d’interaction entre deux rayons lumineux, un rayon ne peut pas en dévier un autre.
Lois de Snell-Descartes
Réflexion
Il y a réflexion lorsque la lumière change brutalement de direction mais tout en restant dans le même milieu de propagation. On distingue deux types de réflexion :
La réflexion métallique où le facteur de réflexion énergétique est proche de 1 : c’est de cette réflexion que l’on parle lorsque la lumière arrive sur un miroir plan, constitué d’une couche métallique déposée sur un support et recouvert d’une plaque de verre.
La réflexion vitreuse : elle se produit lorsque la lumière est interceptée par un dioptre, surface de séparation entre deux milieux transparents. Le facteur de réflexion est plus faible que dans le cas d’une réflexion métallique, puisque outre la lumière réfléchie, il y a une partie qui est transmise (réfractée) dans le second milieu.
Remarque Le coefficient de réflexion dépend dans les deux cas de l’inclinaison des rayons sur la surface réfléchissante. Dans le cas de la réflexion métallique, il dépend aussi de la longueur d’onde de la lumière ; dans le cas de la réflexion vitreuse, il dépend des indices de réfraction des deux milieux.
Lois de la réflexion
Le rayon réfléchi appartient au plan d’incidence défini par la normale au dioptre et le rayon incident ;
Les angles d’incidence \(i_1\) et de réflexion \(i'_1\) vérifient :
\begin{equation}i'_1 = -i_1\end{equation}
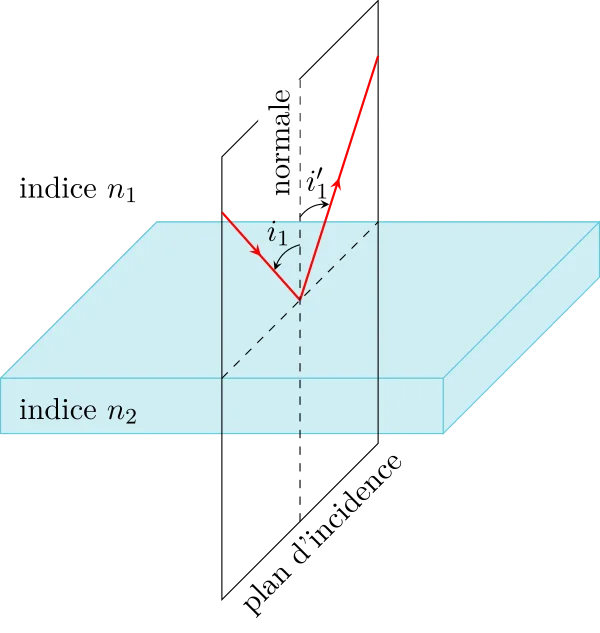
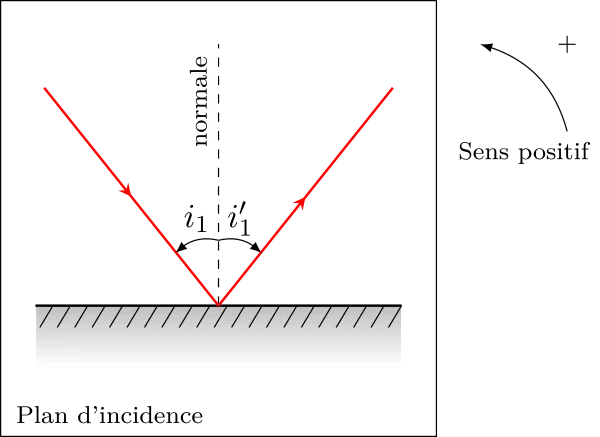
Attention ! Si les angles sont orientés, on doit définir un sens positif et les angles sont des grandeurs algébriques. Ce sens est arbitraire (on le choisit mais on s’y tient). Par contre, les angles sont toujours fléchés à partir de la normale.
Réfraction
Il y a réfraction quand il y a changement de direction de propagation de la lumière lorsque celle-ci traverse un dioptre et change donc de milieu transparent.
Lois de la réfraction
Le rayon réfracté appartient au plan d’incidence.
Les angles d’incidence \(i_1\) et de réfraction \(i_2\) vérifient :
\begin{equation}n_1\;\sin\;i_1 = n_2\;\sin\;i_2\end{equation}
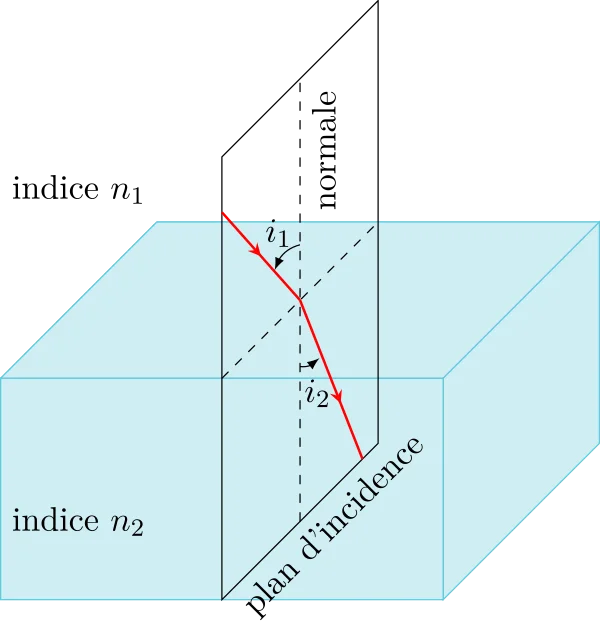
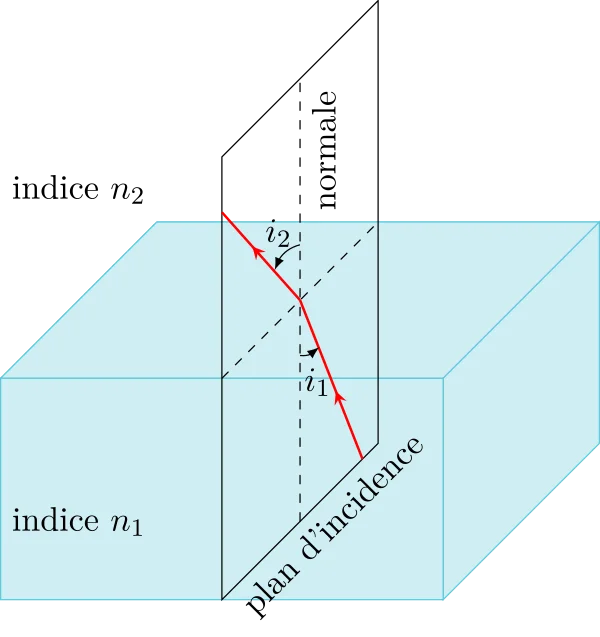
Remarque : le schéma de droite illustre le principe de retour inverse de la lumière par rapport avec le schéma de gauche.
Retour sur la dispersion
Un rayon lumineux va donc changer de direction en changeant de milieu, du fait de la différence d’indice de réfraction. Comme nous l'avons dit précédemment, l’indice de réfraction varie en fonction de la couleur (de la fréquence) de la lumière, on en déduit que l’angle de réfraction ne sera pas le même pour chaque couleur composant une lumière. Les couleurs seront donc dispersées ... le phénomène a lieu avec une seule réfraction mais ne se voit pas très bien. Par contre un dispositif adapté comme un prisme, permet d’obtenir le spectre de la lumière blanche.
Réflexion totale
En vidéo, les caractéristiques de ce phénomène :
Dans le cas de la figure 5 (\(n_1 > n_2\)), à partir d’une certaine valeur de \(i_1\), \(i_2\) peut atteindre \(\pi/2\). A ce moment là, le rayon réfracté n’existe plus, on parle de réflexion totale. A partir de la deuxième loi de Descartes de la réfraction, on trouve l’angle \(i_{1\rm \ell}\) à partir duquel il y a réflexion totale :
\begin{equation}i_{1\rm \ell} = \arcsin{\dfrac{n_2}{n_1}}\end{equation}
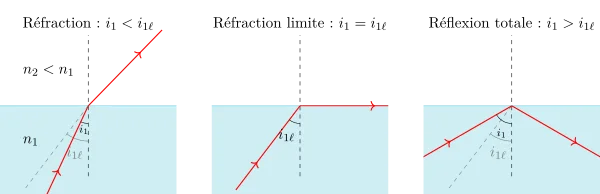
Connaissez-vous des applications de la réflexion totale ? Fibre optique, détecteur de pluie de pare-brise (voir TD), prisme à réflexion totale ou pentaprisme, ...
Réfraction limite
En vidéo, l'explication du phénomène :
Dans l’autre cas, quand le rayon passe d’un milieu moins réfringent à un milieu plus réfringent, l’angle que fait le rayon réfracté \(i_2\) ne peut pas dépasser une certaine valeur correspondant à un angle \(i_1\) de \(\pi/2\). On a alors :
\begin{equation}i_{2\text{max}} = \arcsin {\dfrac{n_1}{n_2}}\end{equation}
Mirages
On appelle mirages des phénomènes optiques lors desquels la lumière ne semble pas se propager en ligne droite comme à l’accoutumée.
Courbure du trajet de la lumière
Dans les milieux inhomogène, l’indice de réfraction n’est pas le même partout. Si on prend par exemple une couche d’air située au dessus de la mer, la partie de la couche très proche de l’eau est plus froide que la partie supérieure de la couche. L’indice de réfraction dépendant de la masse volumique (loi de Gladstone : \(n-1=k\;\rho\), avec $k$ une constante), et l’air froid étant plus dense que l’air chaud, l’indice de réfraction décroît avec l’altitude.
Voici alors ce qu’il arrive :
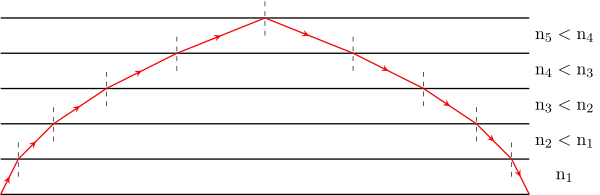
En imaginant que les strates soient très fines, on obtient un trajet courbe.
Les "mirages" classiques : l’eau à la surface de la route, la double île de ré, le rayon vert, la position apparente des étoiles, ...
Application des lois de l'optique géométrique : le prisme
Cette vidéo sur le prisme montre tout d'abord le trajet que suit un rayon lumineux qui pénètre dans le prisme par une de ces faces utiles : il y a donc double réfraction à certaines conditions.
On montre en effet qu'il y a une condition sur l'angle d'incidence pour qu'un rayon qui pénètre soit sur d'émerger. Pour cela on expose ce que sont les trois formules du prisme.
Celles-ci nous servent alors à exprimer la déviation $D$ d'un rayon entre son entrée et sa sortie, elle s'exprime en fonction de l'angle d'incidence $i$, de l'indice de réfraction $n$ du prisme et de son angle au sommet $A$.
Enfin, une étude graphique de la courbe de déviation en fonction de l'angle d'incidence nous permet de montrer que cette déviation passe par un minimum correspondant à la situation où l'angle d'incidence est égal à l'angle de réfraction à la sortie du prisme.
On peut alors exprimer la déviation minimale uniquement en fonction de l'indice de réfaction et de l'angle au sommet du prisme.
En vidéo :
Références
- Pour l'histoire des sciences : Document PHQ399 de David Sénéchal
- "Physique Tout-en-un MPSI PCSI PTSI" - Marie-Noëlle Sanz / Anne-Emmanuelle Badel / François Clausset - Editions Dunod 2008 ;
- "Précis Optique MPSI PCSI PTSI" - P.Brenders / M.Sauzeix - Bréal ;
- Cours sur les lois de l'optique géométrique par Jimmy Roussel
Documents de référence
Derniers ajouts
- Cours 3 de thermo : Interprétation microscopique
- 2ème cours de thermo : transformations - premier principe
- Un premier cours de thermodynamique : Grandeurs thermodynamiques et équations d'états
- Une vidéo sur des bases de mécanique : projection de forces et principe fondamental de la dynamique, PFD et forces de frottements
- Nouvelle série de vidéos de physique pour préparer l'entrée en prépa scientifique : Destination prépa
- Les dernières vidéos de mécanique vont bientôt être mises en ligne, sur les référentiels non galiléens. La playlist est disponible ici
- Le chapitre de mécanique "forces centrales" arrive en vidéos la playlist est disponible ici
- Vidéo de méthodes scientifiques sur la propagation des incertitudes
- Chapitre de mécanique sur le théorème du moment cinétique en vidéos
- Chapitre de mécanique sur les collisions en vidéos
- Chapitre 4 de mécanique : travail et énergies en vidéos
- Chapitre 3 de mécanique : oscillateurs en vidéos
- Chapitre 2 de mécanique : chute avec frottements en vidéos
- On passe à de la mécanique : le chapitre 1 sur la chute libre totalement en vidéo.
- Le dernier chapitre concerne le mouvement des charges dans un conducteur en lien avec le cours 8 d'électromagnétisme
- Série de vidéos sur le cours EM17 où l'on présente les notions d'inductions en lien avec le cours 7 d'électromagnétisme
- Série de vidéos sur le cours EM16 où l'on parle de dipôle magnétique en lien avec le cours 6 d'électromagnétisme
- Série de vidéos sur le cours EM15 qui traite du champ magnétique en lien avec le cours 5 d'électromagnétisme
- Série de vidéos sur le cours EM14 qui traite des conducteurs et condensateurs en lien avec le cours 4 d'électromagnétisme
- Série de vidéos sur le cours EM13 qui traite du dipôle électrostatique en lien avec le cours 3 d'électromagnétisme
- Playlist vidéos sur le cours EM12 sur le potentiel et l'énergie en lien avec le cours 2 d'électromagnétisme
- Playlist vidéos sur le cours EM11 sur le champ électrostatique en lien avec le cours 1 d'électromagnétisme
- Une unique vidéo sur le circuit RLC série en lien avec le cours 3 d'électrocinétique
- Une série de vidéos sur les circuits comportant R, L et C en lien avec le cours 2 d'électrocinétique
- Une série de vidéos sur le régime sinus qui est en lien avec le cours 4 d'électrocinétique
- Un cours assez dense sur la notion de fonction de transfert, des théories de Fourier (décomposition en série et transformée) et des filtres électriques. Ce cours est disponible aussi en vidéos.
- Un cours sur les méthodes numériques (Euler, Runge-Kutta)
- Une vidéo sur l'oeil et ses défauts
- Le cours sur les lois de l'optique géométrique en mp3
- Ensemble de vidéos complémentaires sur le cours 2 de méthodes scientifiques
- Schémas / Figures svg et codes tikz
- Examens en vidéos
- Cours d'électrocinétique sur les résonances du circuit RLC série
- Une vidéo d'électromagnétisme : l'effet Hall
- Une vidéo de mécanique : base polaire, définition et utilisation dans le pendule simple
- Une vidéo de mécanique : méthode d'Euler, explications et exemple
- Une vidéo d'optique : principe du microscope
- Une vidéo d'optique : principe de la lunette astronomique
- Une vidéo d'optique : principe de la lunette de Galilée
- Une vidéo d'optique : Application des lois de l'optique géométrique : le prisme
- Une vidéo d'électrostatique : calcul du champ créé par un fil infini par la méthode intégral
- Cours d'électrocinétique du le régime sinusoïdal
- Résumé de cours sur les notions d'induction
- Résumé de cours sur le circuit RLC série
- Un cours d'électromagnétisme sur quelques notions d'induction
- Une vidéo d'électrocinétique sur le circuit RLC série
- Une vidéo d'électrocinétique sur la charge d'un condensateur
- Deux vidéos sur l'électrostatique : champ, forces et Invariances et symétries
- M14 : travail et énergies
- EC3 : circuit RLC série
- EC2 : condensateur et bobine
- EC1 : lois dans l'ARQS
- M13 : Oscillateurs
- M12 : Chute avec frottements
- M11 : Chute libre
- O14 : Quelques instruments d'optique + résumé
- MS2 : Pratiques de la démarche scientifique + résumé
- MS1 : modélisation en physique + résumé
- M24 : système isolé à deux corps
- TD M24 : TD sur le système isolé à deux corps
- TD M23 : TD sur les changements de référentiels
- M23 : changement de référentiels, référentiels non galiléens
- TD M22 sur les forces centrales
- M22 : mouvement d'un point M soumis à une force centrale
- TD M21 sur le théorème du moment cinétique
- M21 : théorème du moment cinétique
- O2 : généralités sur les systèmes optiques, miroirs
- O1 : lois de l'optique géométrique
- O3 : les lentilles minces
- TD EM7 sur le mouvement de charges dans un conducteur
- EM7 sur le mouvement de charges dans un conducteur
- EM6 sur le dipole magnétique
- TD EM5-EM6 sur le dipole et le champ magnétique
- TD EM4 sur les conducteurs, condensateurs
- EM5 sur le champ magnétique
- EM4 sur les conducteurs en équilibre, les condensateurs
- TD EM3 sur le dipôle électrostatique
- EM3 sur le dipôle électrostatique
- TD EM2 sur le potentiel et l'énergie électrostatiques
- TD EM1 sur le champ électrostatique
- Une ressource pour le programme 2012 de terminale : convertisseur analogique-numérique
- EM2 Potentiel et énergie électrostatique
- EM1 Champ électrostatique
- EM0 Outils mathématiques pour l'électromagnétisme
Physique à l'ENSCR
Retrouver, entre autres, des contenus de travaux pratiques, produits par l'équipe de physique de l'ENSCR


