Licence 1 > Electrocinétique > Cours 3 : Circuit RLC

EC3 : Circuit RLC série

Ce cours est disponible intégralement dans la vidéo que voici :

Introduction

A la fin du chapitre précédent, nous avons étudié les régimes transitoires des circuits du premier ordre RC et RL dont on a résolu les équations différentielles pour trouver les expressions des tensions et intensités.

Nous allons ici étudier dans le même esprit le régime transitoire du circuit RLC série qui comme nous allons le voir donne naissance à des oscillations électriques.

Le circuit RLC étant du deuxième ordre, ce sera aussi le cas de son équation différentielle. Elle fera alors apparaître la notion de régimes : selon l’amortissement du circuit par effet Joule, le régime transitoire est différent.

Vidéo résumé

Équation différentielle

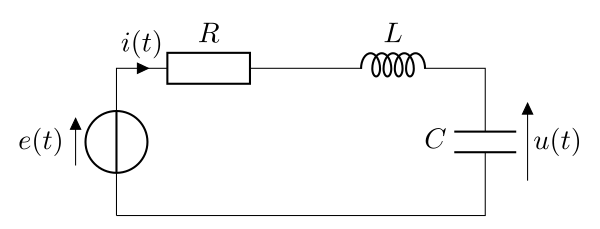
On étudie le circuit RL soumis à une tension \(e(t)\), on s’intéresse à la tension aux bornes du condensateur et à l’intensité qui parcourt le circuit. La bobine est idéale. On applique la loi des mailles  :

\begin{equation}e = Ri + L\dfrac{\mathrm{d}i}{\mathrm{d}t} + u\end{equation}

Comme \(i=C\dfrac{\mathrm{d}u}{\mathrm{d}t}\), on a :

\begin{equation}\boxed{LC\dfrac{\mathrm{d}^2u}{\mathrm{d}t^2} + RC\dfrac{\mathrm{d}u}{\mathrm{d}t} + u = e}\end{equation}

Cette équation différentielle est une équation du second ordre à coefficient constant, le circuit RLC série est appelé circuit du second ordre.

Étude du régime libre

Nous allons nous intéresser dans un premier temps au comportement du circuit lorsque le condensateur à été préalablement chargé sous la tension E du générateur, et lorsqu’il se décharge dans la bobine et la résistance.

L’équation différentielle correspondant à ce régime libre (appelé aussi régime propre) est la suivante :

\begin{equation}\boxed{LC\dfrac{\mathrm{d}^2u}{\mathrm{d}t^2} + RC\dfrac{\mathrm{d}u}{\mathrm{d}t} + u = 0 }\end{equation}

On cherche donc une solution de cette équation qui est une équation homogène. Cette solution est du type \(u=Ae^{rt}\) avec A une constante.
Si on injecte cette solution dans et que l’on élimine la solution \(u=0\) qui n’a pas de sens physique, on obtient :

\begin{equation}LCr^2 u + RC r u + u = 0 \Longleftrightarrow r^2 + \dfrac{R}{L}r + \dfrac{1}{LC} = 0\end{equation}

Cette dernière équation est appelée polynôme caractéristique de l’équation différentielle .
Trouver les solutions de ce polynôme permet de trouver les solutions de l’équation différentielle.

Pour éclaircir la résolution, nous allons utiliser des variables dites "réduites" :

Définitions des variables réduites

L’intérêt des variables réduites est d’utiliser des variables de même dimension dans la résolution de l’équation. On peut donc appliquer sa résolution dans n’importe quel système d’unité.

Pulsation propre

Celle-ci correspond à la pulsation des oscillations en l’absence de "frottements" (amortissement par effet Joule ici) :

En effet, la définition du radian dit que dans un cercle, l’angle en radian est le rapport de la longueur de l’arc que décrit l’angle par le rayon. Il s’agit du rapport de deux longueurs.

Facteur d’amortissement

Il va être lié à la résistance globale du circuit. Plus ce facteur sera grand, plus l’amortissement sera élevé :

Coefficient d’amortissement

Il peut être intéressant de travailler avec une grandeur sans dimension. On définit alors le coefficient d’amortissement par :

\begin{equation}\boxed{\alpha = \dfrac{\lambda}{\omega_0}}\end{equation}

Ce coefficient peut être exprimée en fonction des valeurs des composants du circuit :

\begin{equation}\alpha = \dfrac{R}{2}\sqrt{\dfrac{C}{L}}\end{equation}

Facteur de qualité

Pour caractériser un circuit, on utilise souvent une autre grandeur appelée facteur de qualité. Elle est reliée à toutes les grandeurs dont on vient de parler :

\begin{equation}\boxed{Q = \dfrac{1}{2\alpha}=\dfrac{L\omega_0}{R} = \dfrac{1}{RC\omega_0}}\end{equation}

En utilisant ces variables réduites, on peut donc écrire le polynôme caractéristique de la manière suivante :

\begin{equation}r^2 + 2\lambda r + \omega_0^2 = 0 \hspace{0.5cm}\text{ou} \hspace{0.5cm} r^2 + 2\alpha\omega_0 r + \omega_0^2 = 0\end{equation}

Les différents régimes

Le polynôme caractéristique acceptant plusieurs solutions selon la valeur de son discriminant, il en est de même pour l’équation différentielle.

Vu la forme du polynôme, nous allons utiliser le discriminant réduit.

Ici, le discriminant réduit a pour expression :

\begin{equation}\Delta' = \lambda^2 - \omega_0^2 \hspace{0.5cm} \text{ou} \hspace{0.5cm} \Delta' =\omega_0^2(\alpha^2-1)\end{equation}

Selon son signe on distingue trois régimes :

Régime apériodique : \(\Delta'>0\)

Si \(\Delta'>0\) alors \(\lambda > \omega_0\), \(\alpha>1 \Longleftrightarrow R>2\sqrt{\dfrac{L}{C}}\Longleftrightarrow \boxed{Q<\frac{1}{2}}\)

Racines du polynôme

Le polynôme admet deux racines négatives, on a :

\begin{equation}\begin{aligned} r_1 = -\lambda + \sqrt{\lambda^2-\omega_0^2}= -\alpha\omega_0 + \omega_0\sqrt{\alpha^2-1}\\ r_2 = -\lambda - \sqrt{\lambda^2-\omega_0^2}= -\alpha\omega_0 - \omega_0\sqrt{\alpha^2-1}\end{aligned}\end{equation}

Solution de l’équation différentielle

La solution de l’équation différentielle s’écrit donc :

\begin{equation}u(t) = A_1 e^{r_1t} + A_2 e^{r_2t}\end{equation}

Les racines étant toutes deux négatives, on s’assure que la solution u(t) ne tend pas vers l’infini, cela n’aurait pas de signification physique.

Détermination des constantes

On peut utiliser les conditions initiales pour expliciter les constantes \(A_1\) et \(A_2\). C’est parce que le circuit est du deuxième ordre qu’existent ces deux constantes et qu’il faut deux conditions initiales pour les déterminer.

La continuité de la tension aux bornes du condensateur implique que \(u(t=0)=E\).
La continuité de l’intensité dans la bobine implique que \(i(t=0)=0\).
On obtient alors deux équations à deux inconnues qui nous permettent de déterminer \(A_1\) et \(A_2\) :

\begin{equation}u(t=0) = A_1 + A_2 = E \end{equation}

\begin{equation}\begin{aligned} i(t=0) = r_1 A_1 + r_2 A_2 = 0 \Longleftrightarrow A_2 = -\dfrac{r_1A_1}{r_2} \end{aligned}\end{equation}

On remplace cette expression de \(A_2\) dans :

\begin{equation}\begin{aligned} A_1 -\dfrac{r_1A_1}{r_2} = E \\ \Longleftrightarrow A_1\left(1-\dfrac{r_1}{r_2}\right) = E \\ \Longleftrightarrow \boxed{A_1 = \dfrac{r_2E}{r_2-r_1}}\end{aligned}\end{equation}

On remplace cette expression de \(A_1\) dans l’expression de \(A_2\) de :

\begin{equation}\boxed{A_2 = \dfrac{-r_1E}{r_2-r_1}}\end{equation}

Expression et allure de la tension aux bornes du condensateur

Finalement :

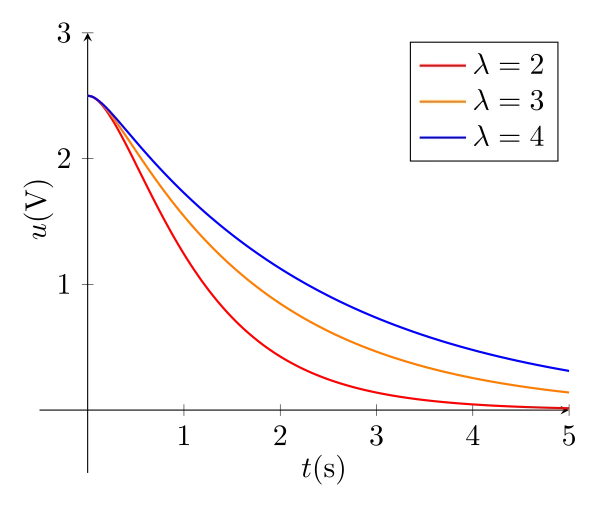
\begin{equation}\boxed{u(t) = \dfrac{r_2E}{r_2-r_1}e^{r_1t} - \dfrac{r_1E}{r_2-r_1}e^{r_2t} }\end{equation}

Lorsque \(\alpha >1 \Longleftrightarrow Q<\frac{1}{2}\), il n’y a pas d’oscillations électrique car l’amortissement est trop fort.

On remarque qu’à t=0, la pente de u(t) est nulle : en effet, \(i(t=0) = C\dfrac{\mathrm{d}u}{\mathrm{d}t}=0\).

Expression et allure de l’intensité dans le circuit

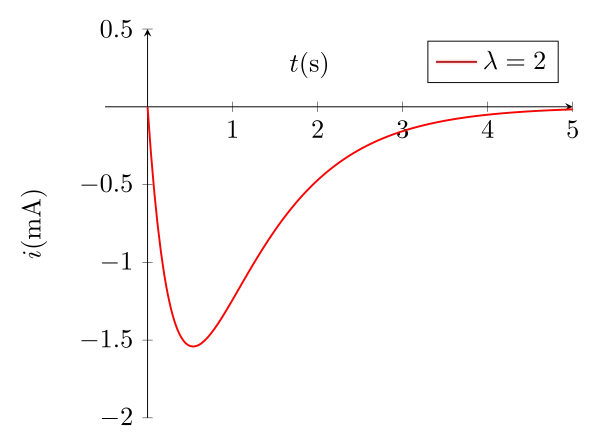
Grâce à la relation \(i(t) = C\dfrac{\mathrm{d}u}{\mathrm{d}t}\), on trouve l’expression de l’intensité :

\begin{equation}\boxed{i(t) = \dfrac{r_2r_1EC}{r_2-r_1}(e^{r_1t} - e^{r_2t})}\end{equation}

Régime critique : \(\Delta'=0\)

Si \(\Delta'=0\) alors \(\lambda = \omega_0\), \(\alpha=1 \Longleftrightarrow R=2\sqrt{\dfrac{L}{C}}=R_C\Longleftrightarrow \boxed{Q=\frac{1}{2}}\)

Racines du polynôme

Le polynôme admet une racine double négative, on a :

\begin{equation}\begin{aligned} r_1 = -\lambda =-\omega_0\end{aligned}\end{equation}

Solution de l’équation différentielle

Alors la solution a pour expression :

\begin{equation}u(t) = (A_1t+A_2)e^{-\lambda t}\end{equation}

Détermination des constantes

On utilise les mêmes conditions que précédemment :

\begin{equation}u(t=0) = E \Longleftrightarrow \boxed{A_2 = E}\end{equation}

On exprime i(t) :

\begin{equation}\begin{aligned} i(t) = -\lambda C (A_1t+A_2)e^{-\lambda t} + A_1 C e^{-\lambda t} = C e^{-\lambda t} \left(A_1 - \lambda (A_1t+A_2)\right)\\\end{aligned}\end{equation}

Et on écrit la condition de continuité :

\begin{equation}\begin{aligned} i(t=0) = A_1 - \lambda A_2 = 0 \\ \boxed{A_1 = \lambda A_2 = \lambda E }\end{aligned}\end{equation}

Expression et allure de la tension aux bornes du condensateur

La solution s’écrit donc :

\begin{equation}\boxed{u(t) = E(\lambda t+1)e^{-\lambda t}}\end{equation}

Le régime critique étant le premier régime apériodique, l’allure de la courbe est identique à celle du régime apériodique, le "retour à l’équilibre" se fait plus rapidement.

Expression et allure de l’intensité dans le circuit

En utilisant la relation \(i(t) = C\dfrac{\mathrm{d}u}{\mathrm{d}t}\), on trouve :

\begin{equation}\boxed{i(t) = -EC\lambda^2te^{-\lambda t} }\end{equation}

De la même manière que précédemment, on retrouve l’allure de l’intensité du courant du régime apériodique.

Régime pseudo-périodique : \(\Delta'<0\)

Si \(\Delta'<0\) alors \(\lambda < \omega_0\), \(\alpha<1 \Longleftrightarrow R<2\sqrt{\dfrac{L}{C}}\Longleftrightarrow \boxed{Q>\frac{1}{2}}\)

Racines du polynôme

Le polynôme admet deux racines complexes conjuguées. Si on pose \(\omega^2 = -\Delta'\), on a :

\begin{equation}r_1 = -\lambda +j\omega \hspace{2cm} r_2 = -\lambda -j\omega\end{equation}

Solution de l’équation différentielle

La solution de l’équation différentielle est la combinaison linéaire de deux solutions complexes :

\begin{equation}u_1(t) = e^{r_1t}=e^{(-\lambda +j\omega)t} \text{ et } u_2 = e^{r_2t}=e^{(-\lambda -j\omega)t} \text{ donnent } u(t) = C_1 e^{r_1t} + C_2 e^{r_2t}\end{equation}

avec \(C_1\) et \(C_2\) des constantes complexes.

Or nous voulons obtenir une solution réelle ! On peut montrer qu’à partir de ces deux solutions complexes, on peut construire deux solutions réelles tout aussi solutions de la même équation différentielle.
Ces deux solutions réelles sont :

\begin{equation}u_3=\dfrac{u_1+u_2}{2} \hspace{2cm} u_4=\dfrac{u_1-u_2}{2j}\end{equation}

Donc :

\begin{equation}\begin{aligned} u_3 = \dfrac{e^{-\lambda t}(\cos \omega t + j \sin \omega t) + e^{-\lambda t}(\cos \omega t - j \sin \omega t)}{2} = e^{-\lambda t}\cos(\omega t)\\ u_4 = \dfrac{e^{-\lambda t}(\cos \omega t + j \sin \omega t) - e^{-\lambda t}(\cos \omega t - j \sin \omega t)}{2j} = e^{-\lambda t}\sin(\omega t)\end{aligned}\end{equation}

La solution réelle de l’équation différentielle est alors une combinaison linéaire de \(u_3\) et \(u_4\) :

\begin{equation}u(t) = (A_1 \cos(\omega t) + A_2 \sin(\omega t))e^{-\lambda t}\end{equation}

avec \(A_1\) et \(A_2\) des constantes réelles.

On trouvera aussi l’écriture suivante qui est équivalente : \(u(t) = A \cos (\omega t + \phi) e^{-\lambda t}\).

Détermination des constantes \(A_1\) et \(A_2\)

Première condition :

\begin{equation}u(t=0) = E \Longleftrightarrow \boxed{A_1 = E}\end{equation}

On exprime i(t) :

\begin{equation}\begin{aligned} i(t) &= C \left(\left(-A_1 \omega \sin (\omega t) + A_2 \omega \cos (\omega t)\right) e^{-\lambda t} - \lambda \left(A_1 \cos (\omega t) + A_2 \sin (\omega t)\right) e^{-\lambda t} \right) \\ &= C e^{-\lambda t} \left( - A_1 \omega \sin (\omega t) + A_2 \omega \cos (\omega t) -A_1 \lambda \cos (\omega t) - \lambda A_2 \sin (\omega t)\right)\end{aligned}\end{equation}

Deuxième condition :

\begin{equation}i(t=0)= A_2 \omega - \lambda A_1 = 0 \Longleftrightarrow \boxed{A_2 = \dfrac{\lambda}{\omega} E}\end{equation}

Expression et allure de la tension aux bornes du condensateur

La solution s’écrit donc :

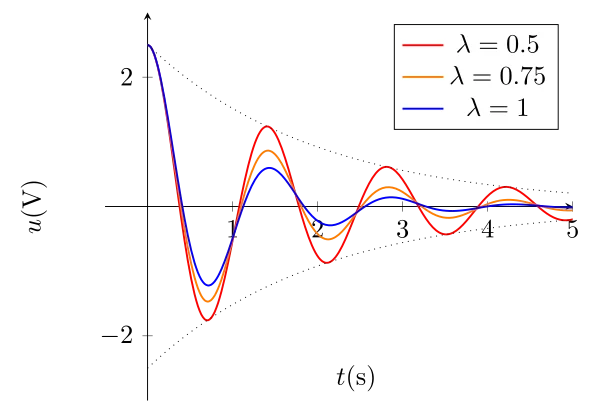
\begin{equation}\boxed{u(t) = E(\cos(\omega t) + \dfrac{\lambda}{\omega} \sin(\omega t))e^{-\lambda t}}\end{equation}

Cette solution se découpe en deux parties :

• Une partie oscillante à la pulsation \(\omega\) ;

• Une amplitude décroissance de manière exponentielle.
  
  

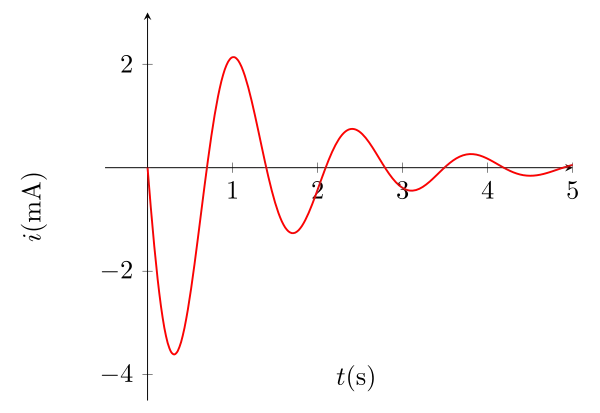
Expression et allure de l’intensité dans le circuit

On a :

\begin{equation}\begin{aligned} i(t) = ECe^{-\lambda t} \left(- \omega \sin (\omega t) +\lambda \cos (\omega t) - \lambda \cos (\omega t) - \dfrac{\lambda^2}{\omega} \sin (\omega t)\right)\end{aligned}\end{equation}

\begin{equation}\boxed{i(t) = -CE (\dfrac{\omega^2 + \lambda^2}{\omega}) e^{-\lambda t} \sin (\omega t) }\end{equation}

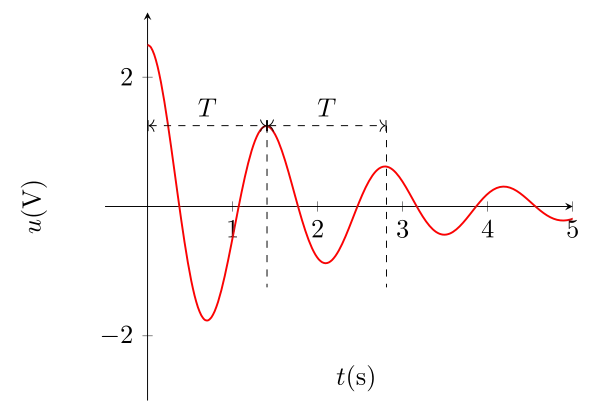
Pseudo-période des oscillations

On observe donc des oscillations électriques à la pulsation \(\omega\), donc de pseudo-période :

\begin{equation}\boxed{T = \dfrac{2\pi}{\omega} = \dfrac{2\pi}{\omega_0\sqrt{1-\alpha^2}} = \dfrac{2\pi}{\sqrt{\omega_0^2-\lambda^2}}} \end{equation}

On parle de pseudo-période car l’amplitude décroît.

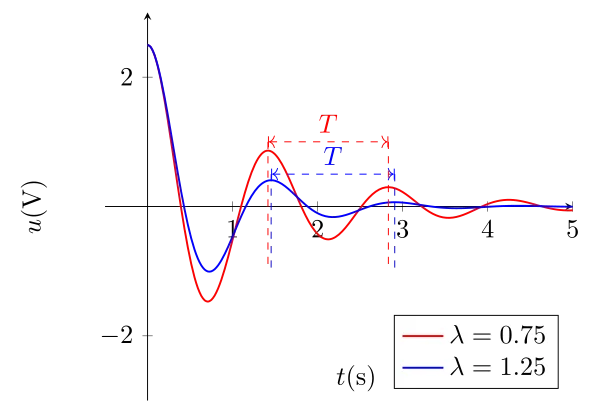
La pseudo-période est voisine mais plus grande que la période propre du circuit (celle qui correspond à un circuit non amorti (R=0)).
Plus l’amortissement est fort (\(\alpha \nearrow\)), plus la pseudo-période s’éloigne de la période propre.

Réponse du circuit RLC série à un échelon de tension

Cette étude ne comporte pas de difficultés même s’il faut veiller à ne pas aller trop vite :

L’équation différentielle concernant la tension aux bornes du condensateur dans ce cas a la forme suivante :

\begin{equation}\boxed{LC\dfrac{\mathrm{d}^2u}{\mathrm{d}t^2} + RC\dfrac{\mathrm{d}u}{\mathrm{d}t} + u = E}\end{equation}

Ainsi, la solution de cette équation sera la somme de la solution de l’équation homogène \(u_1\) (qui sera identique à celle que l’on a trouvé pour le régime libre dans les trois cas) et d’une solution particulière qui est simplement \(u_2=E\). (solution particulière constante car le deuxième membre est constant).

Mais la détermination des constantes de la solution homogène doit être effectuée en tenant compte de la solution particulière. Ainsi :

• On écrira la solution de l’équation homogène avec ces constantes ;

• On lui ajoutera la solution particulière ;

• Et en dernier lieu, on déterminera les constantes avec les conditions initiales.

Aspect énergétique : régime libre

Reprenons la loi des mailles écrites dans ce cas :

\begin{equation}Ri + L\dfrac{\mathrm{d}i}{\mathrm{d}t} + u = 0\end{equation}

Multiplions cette équation par \(i = C\dfrac{\mathrm{d}u}{\mathrm{d}t}\) :

\begin{equation}\begin{aligned} Ri^2 + Li\dfrac{\mathrm{d}i}{\mathrm{d}t} + Cu\dfrac{\mathrm{d}u}{\mathrm{d}t} = 0 \\ \Longleftrightarrow \boxed{Ri^2 + \dfrac{\mathrm{d}\left(\frac{1}{2}Li^2\right)}{\mathrm{d}t} + \dfrac{\mathrm{d}\left(\frac{1}{2}Cu^2\right)}{\mathrm{d}t} = 0} \end{aligned}\end{equation}

Dans cette expression, nous reconnaissons :

• \(Ri^2\) : la puissance dissipée par effet Joule dans la résistance ;

• \(\dfrac{\mathrm{d}\left(\frac{1}{2}Li^2\right)}{\mathrm{d}t}\) : la puissance reçue par la bobine. Elle peut être positive ou négative et correspond aux variations d’énergie magnétique dans la bobine ;

• \(\dfrac{\mathrm{d}\left(\frac{1}{2}Cu^2\right)}{\mathrm{d}t}\) : la puissance reçue par le condensateur. Elle peut être positive ou négative et correspond aux variations d’énergie électrique dans le condensateur.

Pour obtenir les variations énergétiques, on peut intégrer la relation entre \(t=0\) et \(t\rightarrow \infty\). On obtient l’équation \(E_J + \Delta E_C + \Delta E_L = 0\).
Cette relation indique que lorsque l’énergie emmagasinée dans le condensateur va varier, elle va se dissiper par effet Joule en partie, la partie restante étant accumulée par la bobine. Puis la bobine cédera son énergie au condensateur et au conducteur ohmique et ainsi de suite, jusqu’à ce qu’il n’y ait plus d’énergie dans le circuit.