Licence 1 > Electrocinétique > Cours 4 : régime sinusoïdal

EC4 : régime sinusoïdal

Ce cours est disponible intégralement en vidéos dans une playlist Youtube que voici :

Il a été découpé en 5 séquences :

Introduction

Dans les premiers chapitres d’électrocinétique, nous avons travaillé sur les régimes transitoires des circuits comportant conducteur ohmique, bobine et condensateur : on leur appliquait un échelon de tension et regardions l’évolution de la tension et/ou de l’intensité.

Nous allons garder les mêmes circuits, mais cette fois-ci leur comportement sera étudié dans le cas d’un régime variable (les tension et intensité varient au cours du temps) permanent (ces variations sont périodiques).

Après avoir défini les grandeurs électriques en régimes variables, on introduira la notation complexe qui est un outil d’aide à la résolution des équations. Il sera alors temps de parler des résonances du circuit RLC (chapitre EC5) et de filtres électriques (chapitre EC6).

Grandeurs électriques en régimes sinusoïdaux

Écriture mathématique et caractéristiques d’une grandeur sinusoïdale

Les circuits que nous allons étudier serons soumis à une tension sinusoïdale. Graphiquement, on peut dessiner cette fonction ainsi.

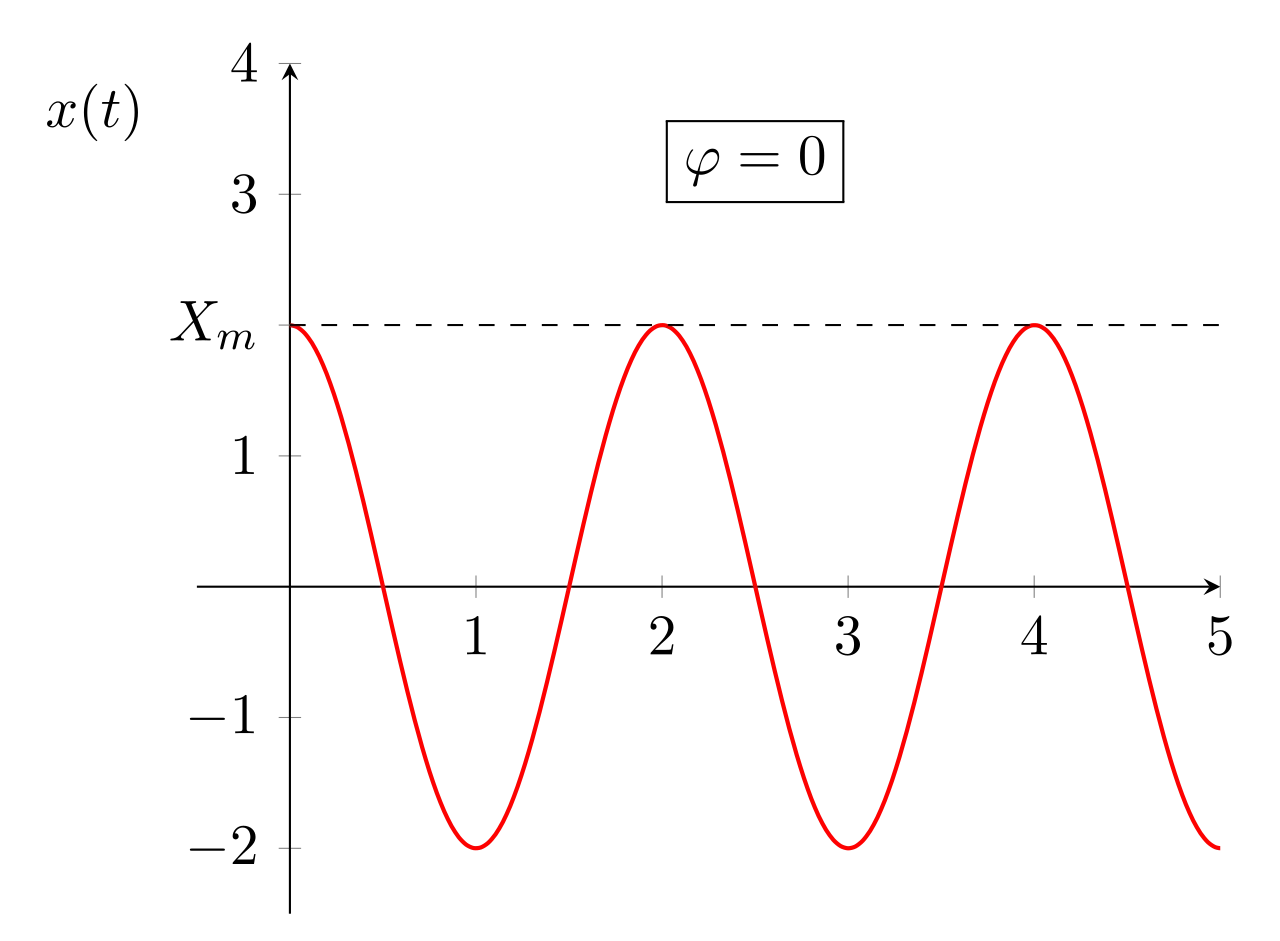
Comment écrit-on mathématiquement ce type de signal ?

Il a la forme suivante :

\begin{equation}x(t)=X_m\cos (\omega t + \phi)\end{equation}

\begin{equation*}\left\{ \begin{array}{lll} X_m \text{ : amplitude du signal ;} \\ \omega \text{ : pulsation en $\mathrm{rad.s^{-1}}$ ;} \\ \phi \text{ : phase à l'origine des dates en $\mathrm{rad}$.} \end{array} \right.\end{equation*}

En effet, sur la figure 1, le signal vérifie $x(t=0) = 0$ et on a nécessairement $\phi = \dfrac{\pi}{2}$.

Remarque

On peut de la même façon utiliser une fonction sinus plutôt qu’une fonction cosinus pour décrire un signal sinusoïdal.

Si on écrit $x(t) = X_m \sin(\omega t +\phi)$ alors pour la figure 1, $\phi = 0$.

Compléments

L’amplitude ne doit pas être confondue avec le signal crête-crête ;
$\omega$ représente la vitesse de périodicité du signal (vitesse que met le signal à reprendre la forme qu’il avait avant).Elle est donc directement reliée à la période T exprimée en seconde et à la fréquence f exprimée en hertz (Hz) :
\begin{equation}\omega = \frac{2\pi}{T} \hspace{2cm} \omega=2\pi f \hspace{2cm} f=\frac{1}{T}\end{equation}
La phase permet de fixer l’origine des temps, la valeur de la grandeur sinusoïdale à t=0.

Déphasage entre deux signaux sinusoïdaux

Cette notion est vue généralement en travaux pratiques et se mesure à l’aide d’un oscilloscope.

On mesure le déphasage entre deux signaux synchrones, c’est à dire de même fréquence.

Définition

Le déphasage est la différence de phase à l’origine des signaux étudiés. Ce déphasage est déterminé au signe près et est généralement compris entre $-\pi$ et $\pi$.

Détermination

Voyons cela sur des exemples :

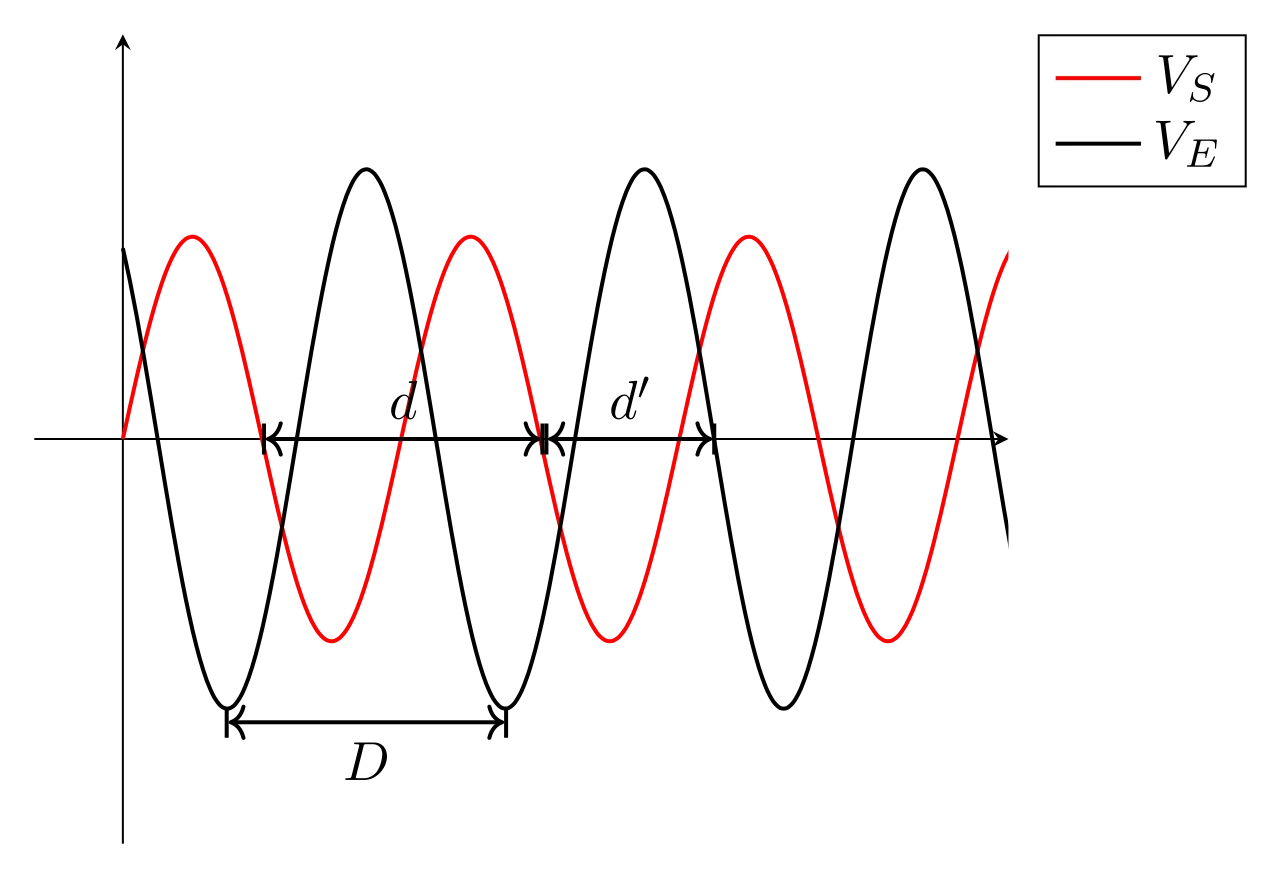
Figure 2 : La tension $V_S$ est en avance sur la tension $V_E$, le déphasage $\Delta \phi$ de $V_S$ sur $V_E$ est positif.

Pour obtenir sa valeur à l’aide d’un oscillogramme, on utilise une règle de trois :Le nombre de division D correspondant à une période des signaux correspond à un déphasage de $2\pi$ ; alors le nombre de division d correspond à un déphasage de $\Delta \phi$ :
\begin{equation}\boxed{\Delta \phi = \dfrac{d\times 2\pi}{D}}\end{equation}

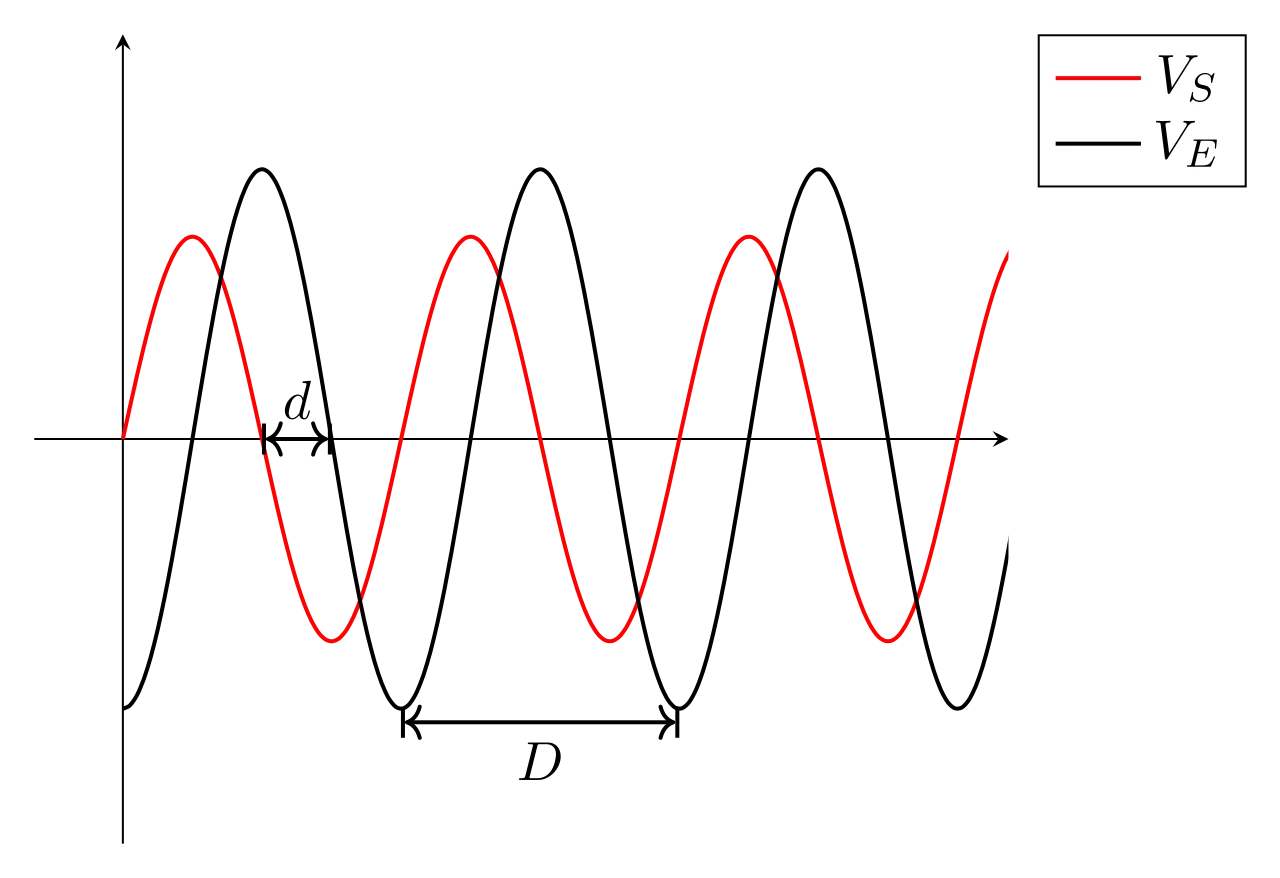
Figure 3 : La tension $V_S$ est en retard sur la tension $V_E$, le déphasage $\Delta \phi$ de $V_S$ sur $V_E$ est négatif.

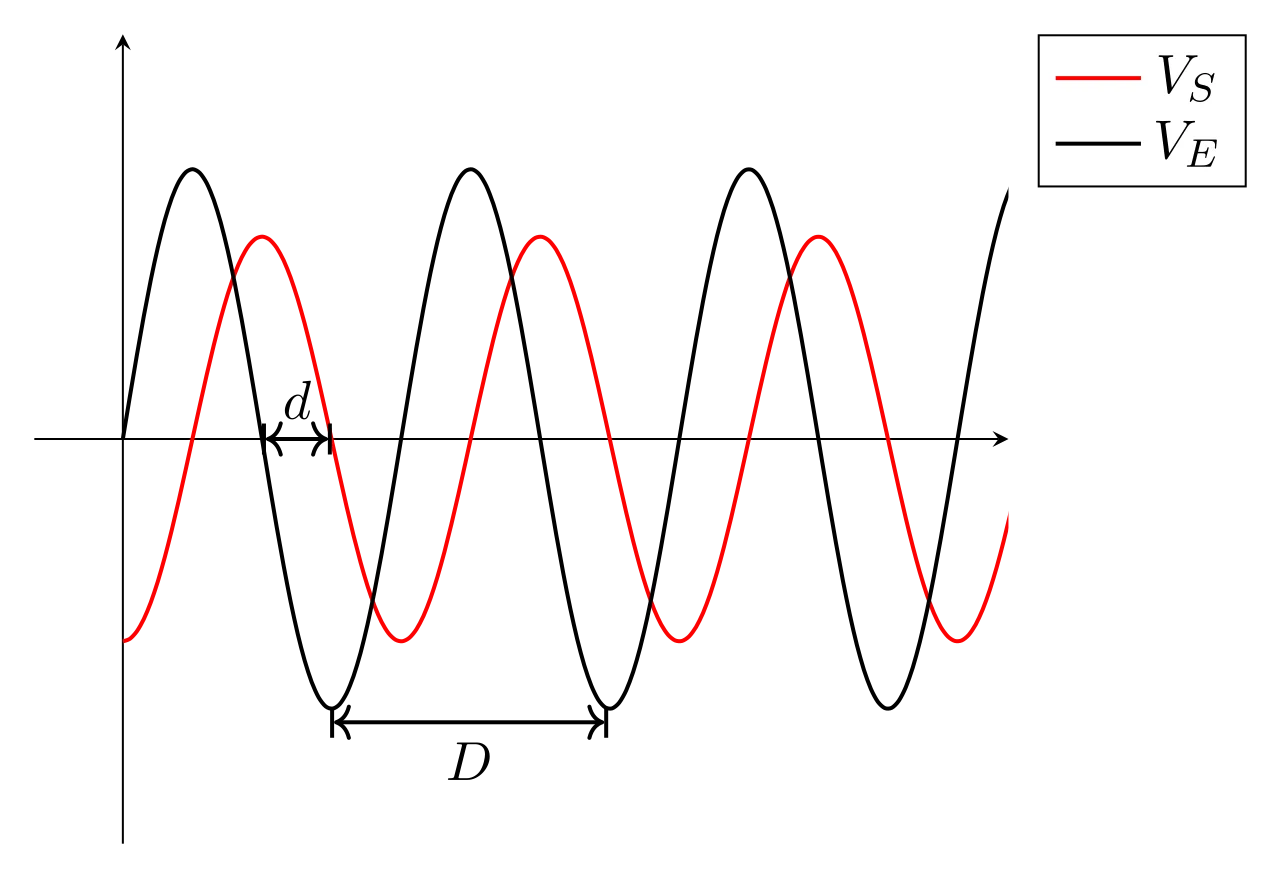
Figure 4 : Si la tension $V_S$ est en avance de plus d’une demie période sur la tension $V_E$, le déphasage $\Delta \phi$ est théoriquement supérieur à $\pi$.On préfèrera plutôt dire que $V_E$ est en avance sur $V_S$ d’un déphasage $\Delta \phi' = 2\pi - \Delta \phi$.

Exemple de déphasage supérieur à pi — Déphasage supérieur à $\pi$

Notation complexe d’un signal périodique

Nous verrons juste après quelques définitions l’intérêt de cette notation complexe.

Rappels mathématiques

Un nombre complexe écrit dans sa forme cartésienne a pour expression :
\begin{equation} z = a + jb \end{equation}
Avec $a$ la partie réelle et $b$ la partie imaginaire, et j le nombre complexe vérifiant $j^2=-1$.
Le module de z noté $|z|$ a pour expression : $|z|=\sqrt{a^2+b^2}$.
Son argument $\theta$ est défini par : $\cos \theta = \dfrac{a}{|z|}$ et $\sin \theta = \dfrac{b}{|z|}$
Un nombre complexe écrit sous sa forme polaire a pour expression :
\begin{equation} z= r(\cos \theta + j\sin \theta) = re^{j\theta} \end{equation}
avec $r = |z|=\sqrt{a^2+b^2}$ son module et $\theta$ son argument.

Définitions

Soit un signal sinusoïdal d’expression mathématique $x(t)=X_m\cos (\omega t + \phi)$, on lui associe une grandeur complexe :

\begin{equation}\underline{x}(t) = X_m e^{j(\omega t + \phi)} = X_m e^{j\omega t} e^{j\phi}\end{equation}

On pourra également définir une amplitude complexe :

\begin{equation}\underline{X}=X_m e^{j\phi} \hspace{0.5cm} \text{donc} \hspace{0.5cm} \underline{x}(t) = \underline{X}e^{j\omega t}\end{equation}

On travaillera donc en notation complexe mais il sera facile de revenir au signal réel :

Retour au signal réel complet grâce à la partie réelle du complexe :
\begin{equation}x(t) = Re(\underline{x}(t))\end{equation}
Retour à l’amplitude du signal réel grâce au module de l’amplitude complexe ou du signal complexe :
\begin{equation}X_m = |\underline{X}| = |\underline{x}(t)|\end{equation}
Retour à la phase initiale grâce à l’argument de l’amplitude complexe :
\begin{equation}\phi = Arg(\underline{X})\end{equation}

Ainsi, toutes les informations dont nous avons besoin pour reconstituer le signal réel sont contenues dans l’amplitude complexe.

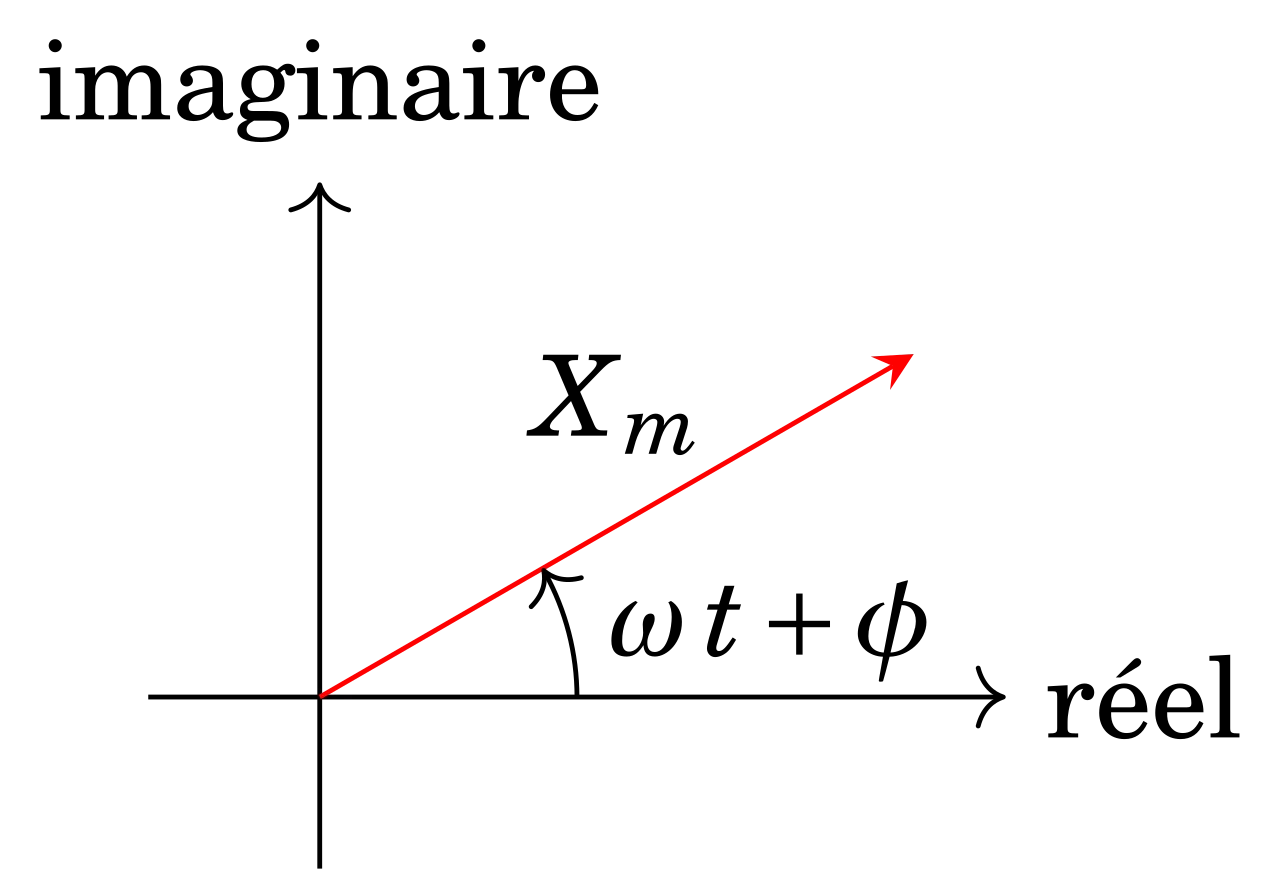
Représentation de Fresnel

Il s’agit d’une représentation vectorielle qui permet une visualisation géométrique de la grandeur sinusoïdale.

A la grandeur $x(t)=X_m\cos (\omega t + \phi)$, on associe dans le plan complexe un vecteur de longueur Xm et dont l’angle avec l’axe horizontal est $\omega t + \phi$.

Représentation de Fresnel d'un signal sinusoïdal

Dérivation de signaux complexes

La présence d’une exponentielle en notation complexe facilite la dérivation du signal :

\begin{equation}\dfrac{d\underline{x}(t)}{dt}=\left(X_m e^{j(\omega t + \phi)}\right)' = j\omega X_m e^{j(\omega t + \phi)} = j\omega \underline{x}(t)\end{equation}

\begin{equation}\boxed{\dfrac{d\underline{x}(t)}{dt}=j\omega \underline{x}(t)}\end{equation}

La dérivée d’un signal complexe est obtenue en multipliant le signal complexe par $j\omega$. Pour une dérivée seconde se sera une multiplication par $(j\omega)^2$...

En effet, vérifions qu’en prenant la partie réelle de la grandeur $j\omega\underline{x}(t)$ on obtient la dérivée du signal réel $x(t)$ :

\begin{equation}\begin{aligned} j\omega\underline{x}(t) &= j\omega X_m e^{j(\omega t + \phi)} = j\omega X_m \cos (\omega t + \phi) + j j\omega X_m \sin (\omega t + \phi)\\ &= - \omega X_m \sin (\omega t + \phi) + j\omega X_m \cos (\omega t + \phi)\\ \text{Donc} \qquad Re(j\omega\underline{x}(t)) &= - \omega X_m \sin (\omega t + \phi)\end{aligned}\end{equation}

La dérivée de x(t) est :

\begin{equation}x(t) = X_m \cos (\omega t + \phi) \Longleftrightarrow \dfrac{dx(t)}{dt}= - \omega X_m \sin (\omega t + \phi)\end{equation}

Intégration de signaux complexes

Sur le même principe, la primitive d’un signal complexe est obtenue en multipliant celui-ci par $\dfrac{1}{j\omega}$ :

\begin{equation}\boxed{\int \underline{x}(t) = \dfrac{1}{j\omega} \underline{x}(t) }\end{equation}

Intérêt de la notation complexe : étude du circuit RC en régime sinusoïdal forcé

Régime forcé

On parle de régime forcé lorsque l’on impose à un circuit une tension sinusoïdale délivrée par un générateur.Après un régime transitoire, le circuit évolue de la même manière que le générateur, notamment à une fréquence identique à celui-ci.

Étude du dipôle RC

Loi des mailles

On étudie le dipôle RC en régime sinusoïdal : un générateur impose aux bornes de ce dipôle la tension $e(t) =E \cos (\omega t + \phi)$.

Circuit RC en régime sinus — Dipôle RC en régime sinusoïdal forcé

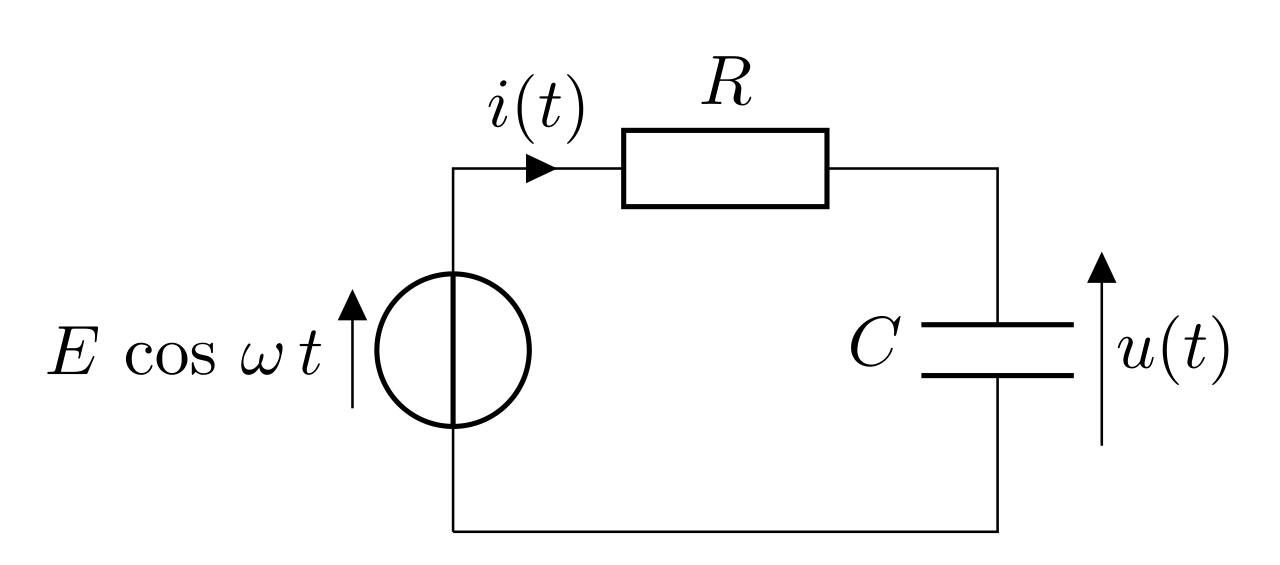
Appliquons la loi des mailles :

\begin{equation}u(t) + R\,i(t) = e(t)\end{equation}

Puis utilisons la notation complexe :

\begin{equation}\underline{u}(t) + R\,\underline{i}(t) = \underline{e}(t)\\\end{equation}

\begin{equation}\Longleftrightarrow \boxed{\underline{u}(t) + R\,\underline{i}(t) = E e^{j(\omega t)}} \end{equation}

Or $i(t) = C\dfrac{du(t)}{dt}$ donc $\underline{i}(t) = C\dfrac{d\underline{u}(t)}{dt} = jC\omega \underline{u}(t)$ (la relation entre $\underline{i}(t)$ et $\underline{u}(t)$ est linéaire).

L’équation devient :

\begin{equation}\underline{u}(t) + jRC\omega \,\underline{u}(t) = E e^{j(\omega t)}\end{equation}

\begin{equation} \Longleftrightarrow \boxed{\underline{u}(t) = \dfrac{E e^{j(\omega t)}}{1+jRC\omega}}\end{equation}

Intérêt de la notation complexe

Ainsi, nous voyons qu’à l’issue de la loi des mailles, il n’y a plus d’équation différentielle à résoudre.

Solution

Posons : $\underline{u}(t) = U e^{j\phi}e^{j\omega t} = \dfrac{E e^{j(\omega t)}}{1+j\tau\omega}$ d’où $\boxed{\underline{U}=U e^{j\phi}= \dfrac{E}{1+j\tau\omega}}$ et $\tau=RC$.

Ainsi, pour obtenir la réponse en tension du circuit, $u(t)$, il faut prendre le module et l’argument de $\underline{U}$ :

En prenant le module de $\underline{U}$, on obtient l’amplitude de $u(t)$ :
\begin{equation}U = |\underline{U}|= \dfrac{|Ee^{j\omega t}|}{|1+j\tau\omega|}=\dfrac{E}{\sqrt{1+\tau^2\omega^2}}\end{equation}
Et pour obtenir la phase à l’origine de $u(t)$(ou son déphasage par rapport à e(t) puisque $\phi_{e(t)} = 0$), on prend l’argument de $\underline{U}$ :
\begin{equation}\phi = Arg(\underline{U}) = Arg(E) - Arg(1+j\tau\omega) = 0 - Arg(1+j\tau\omega)\end{equation}
Alors :
\begin{equation}\tan \phi =- \dfrac{Img(1+j\tau\omega)}{Re(1+j\tau\omega)}= - \tau\omega \end{equation}

Rappels mathématiques

Mais attention, l'expression \eqref{tanphi} peut convenir pour deux angles différents (la tangente définit un angle à $\pi$ près) :

Deux angles pour la même tangente positive — Cercle trigonométrique et tangente

Pour obtenir le signe du cosinus dans notre cas, le plus simple est de réécrire le nombre complexe $\underline{U}$ :

\begin{equation}\underline{U}=\dfrac{E}{1+j\tau\omega} = \dfrac{E(1-j\tau\omega)}{(1+j\tau\omega)(1-j\tau\omega)} =\dfrac{E(1-j\tau\omega)}{1+(\tau\omega)^2}\end{equation}

On a alors :

\begin{equation}\cos \phi = \dfrac{Re(\underline{U})}{|\underline{U}|}=\dfrac{\dfrac{E}{1+(\tau\omega)^2}}{|\underline{U}|} > 0\end{equation}

Donc l’angle est celui contenu dans la partie grisée de la figure ci-contre : $\phi \in \left[-\dfrac{\pi}{2}, 0\right]$. On peut donc écrire $\phi = \arctan(-\tau\omega) = - \arctan{(\tau\omega)}$.

Deux angles pour la même tangente négative

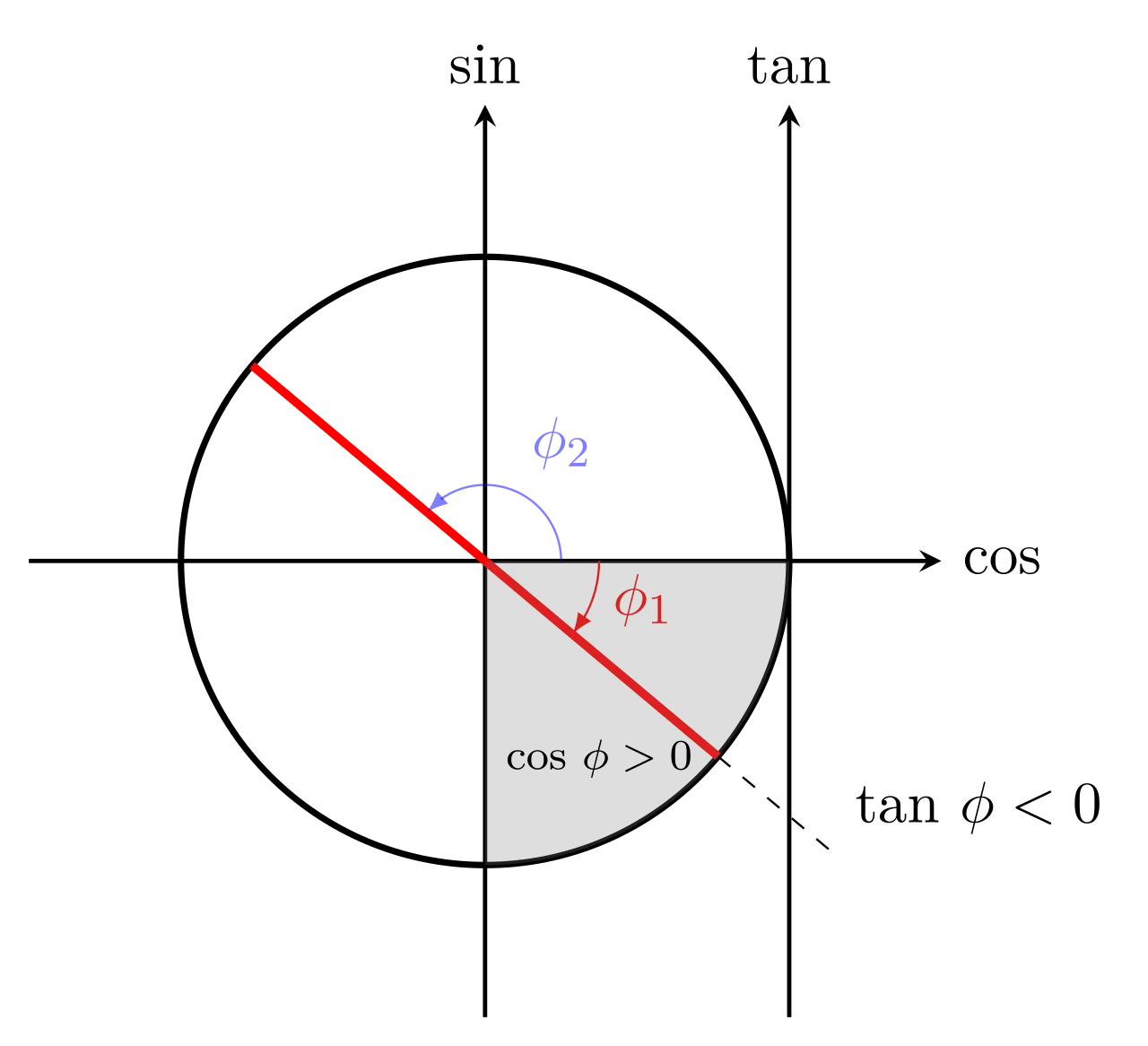
On peut vérifier que pour que $\phi = - \arctan (\tau\omega)$ avec $\tau\omega >0$ donne bien un angle dans l’intervalle négatif.

fonction arctangente et - arctangente — Les fonctions $\arctan{x}$ et $\arctan{-x}$

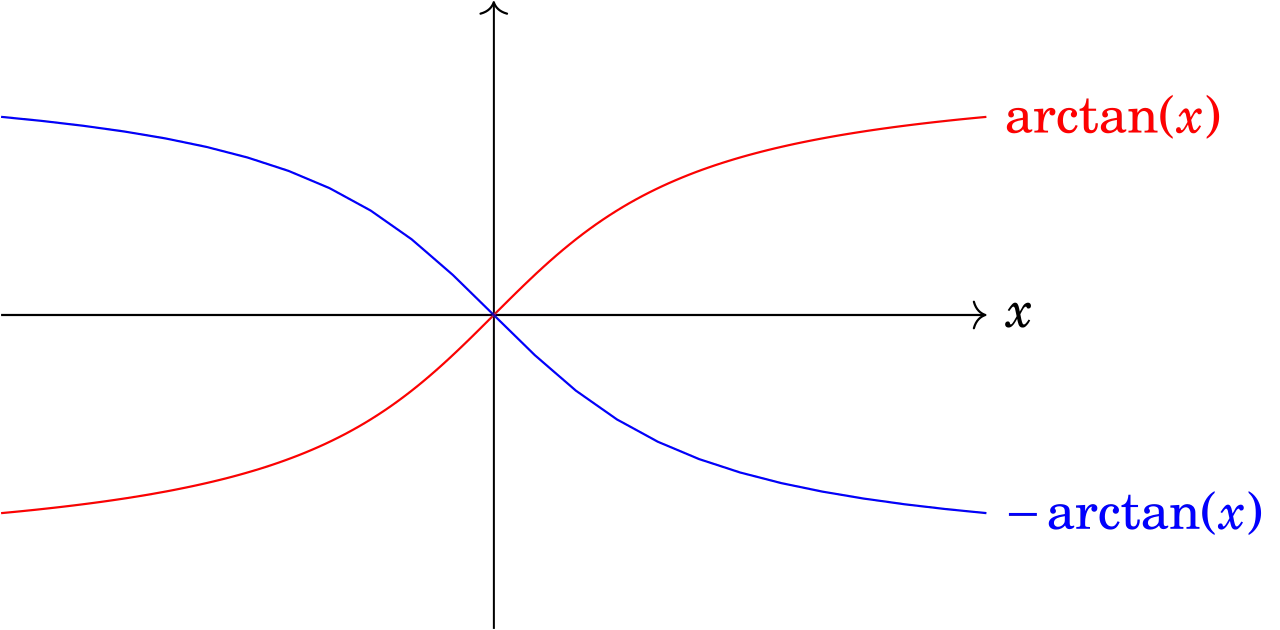
Remarques

Si le cosinus de l’argument $\phi$ avait été négatif, on aurait écrit $ \phi = \pi + \arctan{(-\tau\omega)}$.
Une formule mathématique concernant la fonction arctangente est à connaître :
\begin{equation}\arctan(x) + \arctan\left(\frac{1}{x}\right) = \frac{\pi}{2}\end{equation}
car parfois, selon l’expression complexe utilisée pour obtenir l’argument de $\underline{Z}$, on peut obtenir des résultats différents, visuellement ! en fait ces résultats sont équivalents, on le montre en utilisant la propriété ci-dessus.

Nous avons tout pour écrire $u(t)$ :

\begin{equation}\boxed{u(t) = \dfrac{E}{\sqrt{1+R^2C^2\omega^2}} \cos(\omega t - \arctan (\tau\omega))}\end{equation}

Conclusion

La recherche de cette solution sans passer par la notation complexe aurait fait apparaître des calculs trigonométriques compliqués et nous aurions dû dériver.

Même si la notation complexe demande une certaine gymnastique, les calculs, surtout pour des circuits complexes, seront plus aisés.

Impédance et Admittance complexe

Définitions

Soit une portion de circuit orienté en convention récepteur. En régime sinusoïdal forcé, on utilise une grandeur homogène à une résistance (exprimée donc en ohm ($\Omega$)) qui est le rapport de la tension complexe par l’intensité complexe :

\begin{equation}\boxed{\underline{Z} = \dfrac{\underline{u}}{\underline{i}}}\end{equation}

Cette grandeur est appelée Impédance complexe de la portion de circuit.

On pourra également définir la grandeur inverse, qui sera appelée l’admittance complexe :

\begin{equation}\boxed{\underline{Y} =\dfrac{1}{\underline{Z}} = \dfrac{\underline{i}}{\underline{u}}}\end{equation}

Elle sera homogène à une conductance (exprimée en Siemens (S)).

Exemples des composants R, L et C

Impédance pour un conducteur ohmique

\begin{equation}\underline{Z} = \dfrac{\underline{u}}{\underline{i}} = \dfrac{R\underline{i}}{\underline{i}} = \boxed{R}\end{equation}

Impédance pour un condensateur

\begin{equation}\underline{Z} = \dfrac{\underline{u}}{\underline{i}} = \dfrac{\underline{u}}{C\dfrac{d\underline{u}}{dt}} = \dfrac{\underline{u}}{jC\omega \underline{u}} = \boxed{\dfrac{1}{jC\omega}}\end{equation}

Cette impédance nous permet de définir le comportement du condensateur à basses et hautes fréquences :

En basses fréquences ($\omega \rightarrow 0$), l’impédance du condensateur tend vers l’infini, celle-ci étant homogène à une résistance, on peut dire que le condensateur se comporte comme un interrupteur ouvert.
En hautes fréquences ($\omega \rightarrow \infty$), l’impédance du condensateur tend vers zéro, on peut dire que le condensateur se comporte comme un interrupteur fermé.

Impédance pour une bobine

\begin{equation}\underline{Z} = \dfrac{\underline{u}}{\underline{i}} = \dfrac{L\dfrac{d\underline{i}}{dt}}{\underline{i}} = \dfrac{jL\omega\underline{i}}{\underline{i}} = \boxed{jL\omega}\end{equation}

Cette impédance nous permet de définir le comportement de la bobine à basses et hautes fréquences :

En basses fréquences ($\omega \rightarrow 0$), l’impédance de la bobine tend vers zéro, celle-ci étant homogène à une résistance, on peut dire que la bobine se comporte comme un interrupteur fermé.
En hautes fréquences ($\omega \rightarrow \infty$), l’impédance du condensateur tend vers l’infini, on peut dire que la bobine se comporte comme un interrupteur ouvert.

Loi d’Ohm en notation complexe

L’intérêt de cette impédance complexe réside dans l’écriture d’une loi d’Ohm valable pour nos composants classiques (R,L,C) en régime sinusoïdal forcé.

On pourra donc écrire $\boxed{\underline{u}=\underline{Z}\times\underline{i}}$ pour chaque composant du circuit, ce qui simplifiera les calculs.

Retour aux grandeurs réels

Le module de l’impédance complexe donne le rapport de l’amplitude de la tension par l’amplitude de l’intensité :
\begin{equation}\boxed{Z = |\underline{Z}| = \dfrac{|\underline{u}|}{|\underline{i}|} = \dfrac{U_m}{I_m}}\end{equation}
Si $\underline{u}(t) = U_m e^{j(\omega t + \phi)}$ et $\underline{i}(t) = I_m e^{j(\omega t + \phi')}$.
L’argument de l’impédance complexe donne le déphasage (avance de phase) entre la tension u(t) et l’intensité i(t) :
\begin{equation}\boxed{Arg (\underline{Z}) = Arg (\underline{u}) - Arg(\underline{i}) = \phi - \phi' = \Delta\phi}\end{equation}

Condensateur, bobine et déphasage

Cas de la bobine :

l’impédance a pour expression $\underline{Z}=jL\omega$, calculons le cosinus et le sinus de son argument :

$\cos \Delta\phi = \dfrac{0}{|\underline{Z}|} = 0$

$\sin \Delta\phi = \dfrac{L\omega}{L\omega} = 1$

Ceci implique que $\Delta\phi = \dfrac{\pi}{2}$.

La tension est donc en avance de phase de $\dfrac{\pi}{2}$ sur l’intensité.

Cas du condensateur :

l’impédance a pour expression $\underline{Z}=\dfrac{1}{jC\omega}=-jC\omega$, calculons le cosinus et le sinus de son argument :

$\cos \Delta\phi = \dfrac{0}{|\underline{Z}|} = 0$

$\sin \Delta\phi = \dfrac{-C\omega}{L\omega} = -1$

Ceci implique que $\Delta\phi = -\dfrac{\pi}{2}$.

La tension est donc en retard de phase de $\dfrac{\pi}{2}$ sur l’intensité.

Lois de l’électrocinétique en notation complexe

Les lois que nous avons rencontrées au chapitre EC1 sont valables en notation complexe :

Association en série d’impédance : soit $\underline{Z}_1$ et $\underline{Z}_2$ deux impédances placées en série, alors $\underline{Z}_{eq}$ l’impédance équivalente vérifie :
\begin{equation}\underline{Z}_{eq}=\underline{Z}_1+\underline{Z}_2\end{equation}
Association en parallèle d’impédance : soit $\underline{Z}_1$ et $\underline{Z}_2$ deux impédances placées en parallèle, alors $\underline{Z}_{eq}$ l’impédance équivalente vérifie :
\begin{equation}\dfrac{1}{\underline{Z}_{eq}}=\dfrac{1}{\underline{Z}_1}+\dfrac{1}{\underline{Z}_2}\end{equation}
De même pour la loi des noeuds, la loi des mailles, les ponts diviseurs de courant et de tension, le théorème de Millman.

Puissance en régime sinusoïdal

Valeur efficace d’un signal sinusoïdal

Lorsque l’on mesure la valeur d’une tension sinusoïdale avec un voltmètre en position DC (Direct Composant), celui-ci nous donne sa valeur efficace.

La formule qui permet de calculer la grandeur efficace pour n’importe quel signal périodique est la suivante :

\begin{equation}X_\mathrm{eff}^2 = <x(t)^2> = \dfrac{1}{T}\int_0^T x(t)^2 dt\end{equation}

Où $<x(t)^2>$ est la valeur moyenne de la fonction $x(t)^2$ sur une période.

Dans le cas d’une grandeur sinusoïdale, la grandeur efficace a pour expression :

\begin{equation}\boxed{X_{\mathrm{eff}}=\frac{X_\mathrm{m}}{\sqrt{2}}}\end{equation}

Puissance instantanée

La puissance instantanée reçue par un dipôle à un instant t est définie par $p(t)=u(t)\times i(t)$. Si $u(t) = U_m \cos(\omega t + \phi)$ et $i(t) = I_m \cos(\omega t + \phi')$, alors :

\begin{equation}p(t) = U_m \cos(\omega t + \phi) \times I_m \cos(\omega t + \phi')\end{equation}

Or $\cos\,a \times \cos\,b = \dfrac{1}{2}(\cos(a+b) + \cos(a-b))$, donc :

\begin{equation}p(t) = \dfrac{U_\mathrm{m}I_\mathrm{m}}{2}\left(\cos(2\omega t + \phi + \phi')+\cos(\phi-\phi')\right)\end{equation}

La puissance instantanée oscille deux fois plus vite que la tension et l’intensité (pulsation $2\omega$).

Puissance moyenne et facteur de puissance

On calcule la puissance moyenne par :

\begin{equation}P = \dfrac{1}{T}\int_0^T p(t) dt\end{equation}

L’intégrale sur une période de $\cos(2\omega t + \phi + \phi')$ est nulle. en notant $\Delta\phi = \phi - \phi'$, on a :

\begin{equation}\boxed{P = \dfrac{U_\mathrm{m}I_\mathrm{m}}{2} \cos \Delta\phi = U_{\mathrm{eff}}I_{\mathrm{eff}} \cos \Delta\phi}\end{equation}

Le terme $\cos \Delta\phi$ est appelé facteur de puissance.

Conséquences

La présence du déphasage entre la tension et l’intensité dans l’expression de la puissance moyenne implique que celle-ci est nulle lorsque le déphasage est égale à $\pm\dfrac{\pi}{2}$ : dans le cas d’un condensateur ou d’une bobine, la puissance moyenne reçue est nulle.

Cours en intégralité

EC4 : régime sinusoïdal

Introduction

Grandeurs électriques en régimes sinusoïdaux

Écriture mathématique et caractéristiques d’une grandeur sinusoïdale

Compléments

Déphasage entre deux signaux sinusoïdaux

Définition

Détermination

Notation complexe d’un signal périodique

Définitions

Représentation de Fresnel

Dérivation de signaux complexes

Intégration de signaux complexes

Intérêt de la notation complexe : étude du circuit RC en régime sinusoïdal forcé

Régime forcé

Étude du dipôle RC

Loi des mailles

Intérêt de la notation complexe

Solution

Conclusion

Impédance et Admittance complexe

Définitions

Exemples des composants R, L et C

Impédance pour un conducteur ohmique

Impédance pour un condensateur

Impédance pour une bobine

Loi d’Ohm en notation complexe

Retour aux grandeurs réels

Condensateur, bobine et déphasage

Cas de la bobine :

Cas du condensateur :

Lois de l’électrocinétique en notation complexe

Puissance en régime sinusoïdal

Valeur efficace d’un signal sinusoïdal

Puissance instantanée

Puissance moyenne et facteur de puissance

Conséquences

Documents de référence

Derniers ajouts

Liens

Physique à l'ENSCR