Licence 1 > Thermodynamique > Cours 1 : grandeurs thermodynamiques et équations d'état
T1 : Grandeurs thermodynamiques - équations d'états
Système thermodynamique
Région de l’espace qui contient un corps délimité par une frontière. On appelle l’extérieur tout ce qui n’appartient pas au système.
On ne peut pas utiliser la mécanique pour trouver les positions et les vitesses de chaque particule du corps à chaque instant, il y a beaucoup trop de paramètres à calculer. On utilise alors la thermodynamique, qui définit des grandeurs macroscopiques (pression, température, volume, masse, masse volumique, nombre de moles, etc) qui vont permettre de rendre compte de l’état du système. Ces grandeurs macroscopiques s’appellent variables d’état.
Différents types de système En thermodynamique, on parlera de système :
isolé : il n’échange pas d’énergie ni de matière avec l’extérieur ;
fermé : il peut échanger de l’énergie mais pas de matière avec l’extérieur ;
ouvert : énergie et matière peuvent être échangés entre le système et l’extérieur.
Variables externes et internes
Variables externes : variables que l’on peut contrôler de l’extérieur : on peut imposer à une enceinte munie d’un piston un certain volume $V$ ou une certaine température $T$.
Variables internes : variables qui va s’ajuster selon les conditions extérieurs, la pression est de celles là, si on impose un volume à l’enceinte, la pression du gaz à l’intérieur est modifiée.
Variables intensives et extensives
Lorsque duplique un système thermodynamique, les variables extensives sont doublées (par exemple le nombre de molécules) alors que les variables intensives ne le sont pas.
Variables extensives : nombre de molécules, masse totale, volume
Variables intensives : pression, température, concentration, masse volumique
Equilibre thermodynamique
Un système thermodynamique isolé finit toujours pas atteindre un état stable dans lequel les variables d’état sont constantes, dit état d’équilibre. Cet état est unique.
Un système non isolé peut être dans un état d’équilibre pendant une certaine durée tant que ses variables d’état sont constantes sur cette durée.
Principe 0 de la thermodynamique
Si A est en équilibre avec B et que B est en équilibre avec C, alors A est en équilibre avec C.
Pression
\begin{equation}\boxed{p = \dfrac{F}{S}}\end{equation} p s’exprime en Pascal (Pa), unité SI. Elle peut aussi s’exprimer en bar ($1\,\mathrm{bar} = 1 \times 10^{5}\,\mathrm{Pa}$). Elle peut aussi s’exprimer en millimètre de mercure (760 mm d’Hg $=1{,}013 \times 10^{5}\,\mathrm{Pa}$ $\Longleftrightarrow 1\,\mathrm{mm\,d'Hg} = 133{,}33\,\mathrm{Pa}$).
Masse volumique
Pour un corps homogène \begin{equation}\boxed{\rho = \dfrac{m}{V}}\end{equation} Elle s’exprime en $\mathrm{kg.m^{-3}}$.
Valeurs de référence : $\rho_\mathrm{eau} = 1000\,\mathrm{kg.m^{-3}}$ ; $\rho_\mathrm{air} = 1{,}2\,\mathrm{kg.m^{-3}}$ à 20°C.
Densité particulaire
C’est le nombre de particules par unité de volume : \begin{equation}\boxed{n^*=\dfrac{\rho}{m_0}}\end{equation} avec $m_0$ la masse d’une particule en kilogramme (kg). La densité particulaire s'exprime donc en $\mathrm{m^{-3}}$.
Ordres de grandeurs intéressants :
Milieu interstellaire : $1\,\mathrm{cm^{-3}}$
Milieu intergalactique : $1\,\mathrm{m^{-3}}$
Quantité de matière
On note $n$ celle-ci, elle s’exprime en moles (mol). Elle vaut : \begin{equation}\boxed{n = \dfrac{N}{\mathcal{N_A}}}\end{equation} Où $\mathcal{N_A}$ est le nombre d’Avogadro, c’est à dire le nombre d’entités (atomes, molécules, ions, etc) par mole. Pour une mole, il y a $\mathcal{N_A} = 6{,}023\times 10^{23}$ entités.
Température en degré (Celsius, ou Fahrenheit)
L’échelle de température Celsius, appelé degré Celsius, a été définie en fixant la température de deux points fixes, le 0°C et le 100°C. Entre ces deux points, on a découpé l’échelle en 100 subdivisions d’où la notion de degré.
Fahrenheit définit son échelle en fixant également la valeur de la température du mélange eau + glace (0°C) qu’il fixe à 32°F. En effet, il ne voulait pas de température négative, et il souhaitait un nombre ayant beaucoup de multiples. Pour le point le plus haut (ébullition de l’eau), il choisit 212°F, qui correspond à 32+180! il divise alors son échelle en 180°F.
Equations d’état
Soit un système thermodynamique, décrit par ses variables d’état $p$, $T$, $V$, $n$. Plusieurs lois ont été établies au cours de l’histoire :
Loi de Boyle-Mariotte (1662)
Le produit $p\,V$ est indépendant de $p$ à $T$ fixée.
Loi de Charles (1787)
A pression constante et pour des faibles pressions : \begin{equation}\boxed{V = V_0(1+\alpha\,t)} \end{equation} $\text{avec} \quad \alpha = \dfrac{1}{273{,}15}$ et $V_0$ est volume de référence, et la température $t$ exprimée en °C.
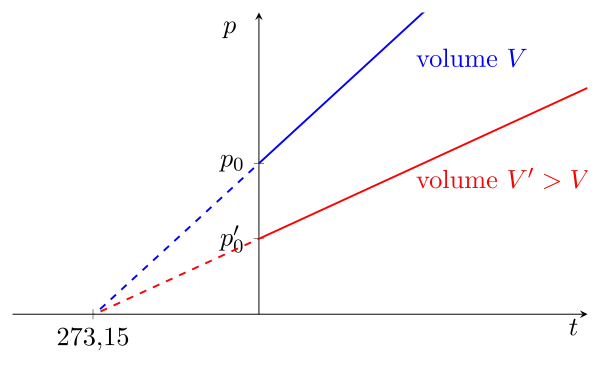
Si on prolonge le graphe précédent, on se rend compte que le volume devient nul pour une certaine température. On obtient : \begin{equation}V = V_0(1+\alpha\,t)=0 \Longrightarrow (1+\alpha\,t)=0 \Longrightarrow t = -\dfrac{1}{\alpha} = -273{,}15\,\mathrm{^\circ C}\end{equation} On pressent que cette température va jouer un rôle par la suite.
On peut noter également que si la courbe $V=f(t)$ est tracée sous une autre pression par exemple plus grande, donc avec un volume de référence plus petit, la courbe tend toujours vers la même température à volume lorsque le volume est nul.
En décalant notre échelle de température, on définit en réalité une nouvelle température dite absolue en Kelvin : \begin{equation}\boxed{T = t + 273{,}15\,\mathrm{^\circ C}}\end{equation} Alors en remplaçant $t$ par $T$ dans la loi de Charles, la relation entre volume et température absolue s’écrit \begin{equation}\boxed{V = \mathrm{cste(p)}\,T}\end{equation} Le volume est proportionnel à la température absolue (la constante de proportionnalité dépend de la pression).
La loi de Gay-Lussac (1802)
Elle est identique à la loi de Charles, mais s’écrit en terme de pression. Soit, à volume constant : \begin{equation}p = p_0\,(1 + \alpha\,t)\end{equation} avec $p_0$ une pression de référence, la température $t$ exprimée en °C, et $\alpha$ le même coefficient que celui de la loi de Charles.
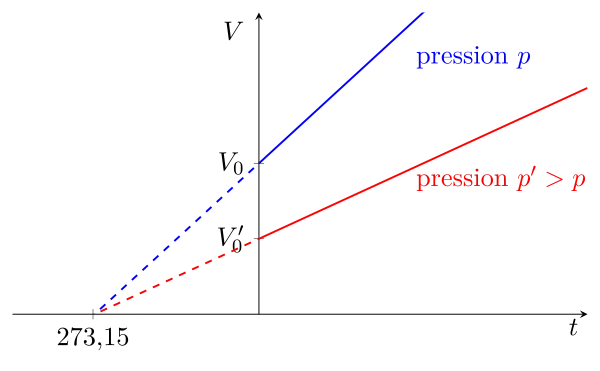
Cette loi peut également être écrite en fonction de la température absolue, on obtient donc également une relation de proportionnalité : \begin{equation}\boxed{p = \mathrm{cste(V)}\,T}\end{equation} La constante dépend du volume.
Combinaison des lois de Charles et Gay-Lussac
Finalement, si on combine les lois de Charles et de Gay-Lussac, on peut écrire que le produit $p\,V$ : \begin{equation}\begin{cases} p\,V = p\,\mathrm{cste}(p)\,T \\ p\,V = V\,\mathrm{cste}(V)\,T \end{cases} \Longrightarrow p\,V = \mathrm{cste}\times T\end{equation} On retrouve la loi de Boyle-Mariotte, le produit $p\,V$ est proportionnelle à la température, ici la température absolue.
Loi d’Avogadro-Ampère (1811-1814)
Elle a été énoncée indépendamment par les deux scientifiques, en 1811 pour le premier et 1814 pour le deuxième.
Son énoncé est le suivant : à pression et température données, le volume d’un gaz est proportionnelle à sa quantité de matière. On peut également dire que le volume molaire d’un gaz est constant : \begin{equation}\boxed{\dfrac{V_1}{n_1} = \dfrac{V_2}{n_2}}\end{equation} avec $V_1$,$V_2$ le volume du gaz n°1{,}2 ayant la quantité de matière $n_1$,$n_2$.
On peut enfin l’écrire en terme de produit $p\,V$ : la loi signifie que $p\,V$ est proportionnel à $n$.
Retour sur la valeur de 273,15 : température absolue en Kelvin
Expérimentalement, on remarque quelques écarts à la loi de Boyle-Mariotte, en effet si on trace la courbe $p\,V = f(p)$ à des températures données, on ne trouve pas des droites horizontales mais légèrement décroissantes :
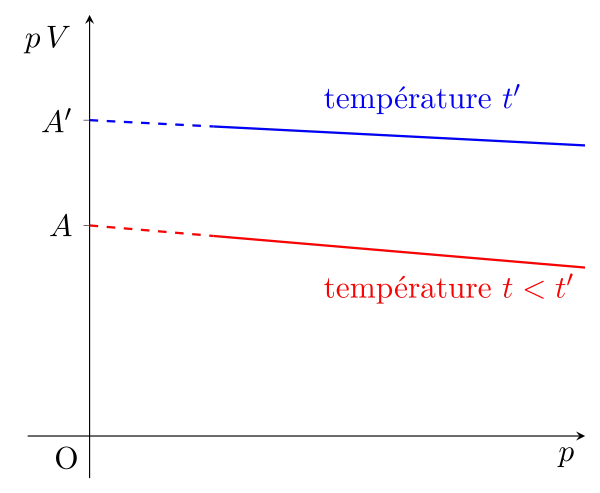
Alors si on regarde l’ordonnée à l’origine des courbes, c’est à dire à pression évanouissante, on observe que la différence de ces ordonnées est indépendante du gaz et que leur rapport est constant : \begin{equation}\dfrac{\mathrm{OA'}}{OA} = \mathrm{cste} \quad \text{et en particulier} \quad \dfrac{\mathrm{OA_{100^\circ}}}{\mathrm{OA_{0^\circ}}} = 1{,}3661\end{equation}
On définit alors la température absolue en Kelvin à l’aide de ce rapport : \begin{equation}\dfrac{T'}{T} = \dfrac{\mathrm{OA_{100^\circ}}}{\mathrm{OA_{0^\circ}}} = 1{,}3661\end{equation}
On a également souhaité conserver l’écart de 100 entre la température de fusion de la glace et la température d’ébullition de l’eau. Nous avons donc deux conditions pour construire la température en Kelvin : \begin{equation}\begin{cases} \dfrac{T_{100}}{T_0} = 1{,}3661 \\ T_{100} = T_0 + 100 \end{cases} \Longrightarrow \quad T_0 = 273{,}15\,\mathrm{K} \quad \text{et} \quad T_{100} = 373{,}15\,\mathrm{K}\end{equation}
Définition de la température absolue en Kelvin
La mesure de la température absolue en kelvin est indépendante de l’instrument et du fluide utilisé pour construire le thermomètre. Elle est défini par : \begin{equation}\boxed{T(K) = t(^\circ C) + 273{,}15}\end{equation} On ne parle pas de degré Kelvin puisque cette température n’a pas été construit via une échelle de mesure (subdivisions d’un intervalle de température entre deux points caractéristiques de température connue.)
Modèle du gaz parfait
\begin{equation}\boxed{p\,V = n\,R\,T}\end{equation} est l’équation d’état d’un modèle de gaz dit parfait. Il est valable pour certains gaz :
dans un milieu peu dense, à température pas trop basse et pression pas trop élevée;
dans lequel les particules sont considérées comme ponctuelles;
et pour lequel on considère qu’il n’y a pas d’interaction entre les molécules du gaz
$R$ est la constante des gaz parfaits et vaut $8{,}314\,\mathrm{J.K^{-1}.mol^{-1}}$.
Mélange de gaz parfaits
Soit un gaz composé de plusieurs molécules différentes, on note $n_i$ le nombre de moles de gaz de l’espèce $i$, alors :
On appelle fraction molaire la grandeur \begin{equation}x_i = \dfrac{n_i}{n_\mathrm{totale}}\end{equation} Par exemple dans l’air, $x_\mathrm{N_2} = 78\%$, $x_\mathrm{O_2} = 21\%$
On appelle pression partielle $p_i$ la grandeur : \begin{equation}p_i = x_i\,p_\mathrm{totale} = \dfrac{n_i}{n_\mathrm{totale}}\,p_\mathrm{totale}\end{equation} Par exemple dans l’air, $p_\mathrm{N_2} = 0{,}78 \times 10^{5}\,\mathrm{Pa}$
Un mélange sera qualifié d’idéal lorsque les molécules des gaz présents dans ce mélange n’interagissent pas entre elles.
La loi de Dalton s’applique à ces mélanges : Dans un mélange idéal, la pression partielle d’un gaz est celle qui l’aurait s’il était le seul constituant à occuper tout le volume.
La température : température du gaz parfait
La loi des gaz parfaits permet de définir la notion de température sans ambiguïté : \begin{equation}T = \dfrac{p\,V}{n\,R}\end{equation} Ainsi on définit la température d’un corps comme étant la température du gaz parfait en équilibre thermodynamique avec ce corps.
Initialement, le Kelvin était défini comme la fraction $\dfrac{1}{273{,}16}$ de la température thermodynamique du point triple de l’eau (ce point triple est le point pour lequel les trois phases de l’eau, solide, liquide et gaz, coexistent). Le $0\,\mathrm{K}$, égale à $-273{,}15^\circ\,C$, correspond au zéro absolu. le point triple de l’eau correspond à $0{,}01^\circ\,C$.
Nouvelle définition du Kelvin (à partir du 20 mai 2019)
Un kelvin est désormais égal au changement de la température thermodynamique résultant d’un changement de l’énergie thermique $k_B\times T$ de $1{,}380649 \times 10^{-23}\,\mathrm{J}$.
Ecart au gaz parfait : modèle de Van der Waals
Si on regarde l’évolution du produit $p\,V$ en fonction de $p$ (diagramme d’Amagat) d’un gaz, aux pressions non évanouissantes (c-à-d aux pressions plus grandes), le tracé d’une isotherme ne donne plus une droite.
Van der Waals propose en 1873, d’ajouter deux termes correctifs à l’équation d’état des gaz parfaits pour prendre en compte le volume non négligeable des molécules et l’interaction entre celles-ci.
\begin{equation}\boxed{\left(p + \dfrac{n^2\,a}{V^2}\right)(V - n\,b) = n\,R\,T}\end{equation}
avec :
$b$ le covolume, $n\,b$ représente le volume minimal occupé par les molécules;
$\dfrac{n^2\,a}{V^2}$ la pression moléculaire, qui traduit l’existence de forces attractives entre les molécules, la pression exercée par un gaz réel est moins forte que celle exercée par un gaz parfait dans les mêmes conditions du fait de ces forces.
Modèle de Van der Waals
Si les gaz présentent un écart aux gaz parfaits, on peut utiliser le modèle plus sophistiqué de Van der Waals: \begin{equation*} \boxed{\left(p + \dfrac{n^2\,a}{V^2}\right)(V - n\,b) = n\,R\,T} \end{equation*} avec $n^2\,a/V^2$, la pression moléculaire et $b$ le covolume.Ressources :
"Physique Tout-en-un MPSI PCSI PTSI" - Marie-Noëlle Sanz / Anne-Emmanuelle Badel / François Clausset - Editions Dunod 2008 ;
https://www.youtube.com/@physiqueprepa ; cours de thermodynamique de Nicolas Hergott
http://demonstrations.wolfram.com/StatisticalNatureOfMaxwellBoltzmannDistribution/
https://www.futura-sciences.com/sciences/definitions/physique-kelvin-353/


