Licence 1 > Optique 1 > Cours 3 : lentilles minces
O3 : les lentilles minces
Introduction
Nous allons aborder ce chapitre comme la partie sur les miroirs du chapitre précédent : après avoir défini une lentille et les différents types de lentilles, nous nous intéresserons aux grandeurs caractéristiques de celles-ci, puis aux formules de conjugaison et grandissement. On présentera ensuite toutes les constructions possibles ainsi que la construction d’un rayon émergent correspondant à un rayon incident donné. Enfin, nous nous intéresserons aux similitudes et différences entre lentilles et miroirs, notamment en parlant de leur défauts (aberrations).
Différents types de lentilles
Définition d’une lentille
Une lentille est un milieu transparent limité par deux dioptres, les deux peuvent être sphériques ou l’un est sphérique et l’autre est plan (on les nomme souvent lentilles sphériques).
Nous étudierons le cas des lentilles minces : une lentille est mince si son diamètre est très grand devant son épaisseur.
Rigoureusement, si on appelle \(\text{R}_1\) le rayon du premier dioptre sphérique de la lentille, \(\text{R}_2\) le rayon de son deuxième dioptre et si e est l’épaisseur de la lentille ; toute lentille est mince à conditions que \(e<<\text{R}_1\), \(e<<\text{R}_2\) et \(e<<|\text{R}_1-\text{R}_2|\) .
Nous n’oublierons pas que la lentille mince sphérique a la propriété de changer la direction de propagation de la lumière du fait de la réfraction qui se produit sur chaque dioptre de celle-ci.
Deux types de lentilles
On distingue deux types de lentilles, celles à bords minces et celles à bords épais. Les premières sont convergentes, les secondes sont divergentes.

Points particuliers et grandeurs caractéristiques
Les lentilles sphériques, comme les miroirs sphériques, ne sont pas des systèmes optiques rigoureusement stigmatiques et aplanétiques. Comme pour le miroir, on peut montrer que des rayons arrivant parallèles sur toute la hauteur de la lentille ne convergent pas en un seul point.
Cependant, si les lentilles sont utilisées dans les conditions de Gauss définies dans le chapitre précédent, on parle de stigmatisme et aplanétisme approchés.on pourra alors définir la notions de foyers.
Centre optique
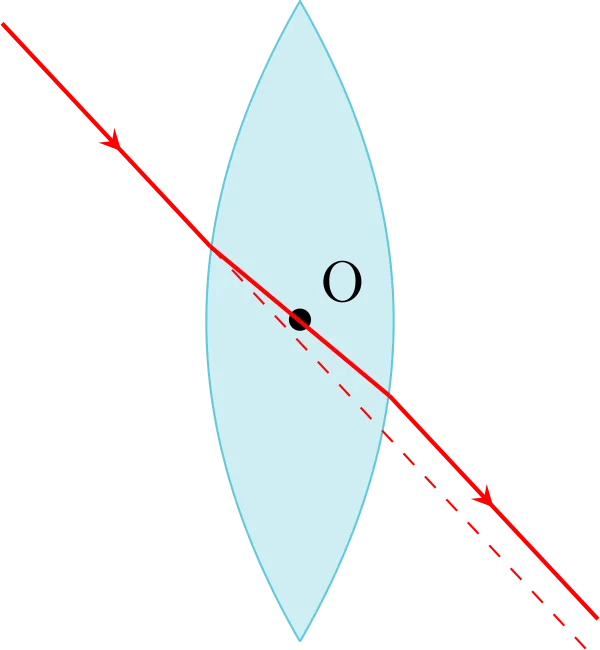
On appelle centre optique de la lentille, noté O, le point de l’axe optique de la lentille par lequel passe le rayon réfracté correspondant à un rayon incident dont le rayon émergent correspondant lui est parallèle.
Foyers
Cas d’une lentille convergente
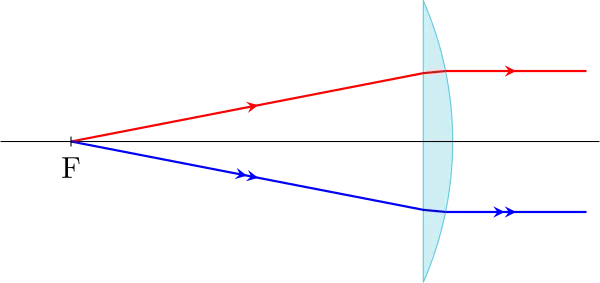
Une lentille convergente comporte deux foyers, appelés foyer principal objet et foyer principal image :
Tout rayon incident passant par F, foyer principal objet, émerge parallèle à l’axe optique. Ce foyer a donc son image à l’infini ;
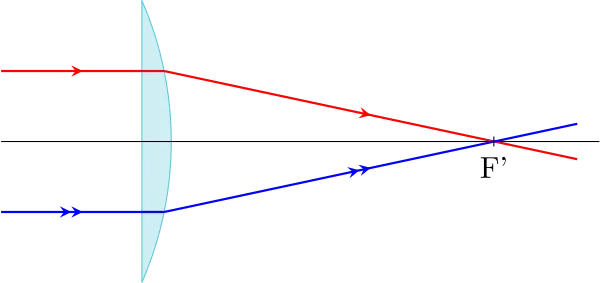
Tout rayon incident parallèle à l’axe optique émerge en passant par F’, foyer principal image. Ce foyer est donc l’image d’un objet à l’infini ;
Ces foyers sont symétriques par rapport au centre optique de la lentille.
Remarque Rappelons que le plan transverse à la lentille qui passe par F’ est appelé plan focal image. Des rayons parallèles mais inclinés par rapport à l’axe optique se croisent en un point, appelé foyer secondaire image, de ce plan focal image.De même avec le plan focal objet, ce sera également le cas avec les lentilles divergentes.
Cas d’une lentille divergente
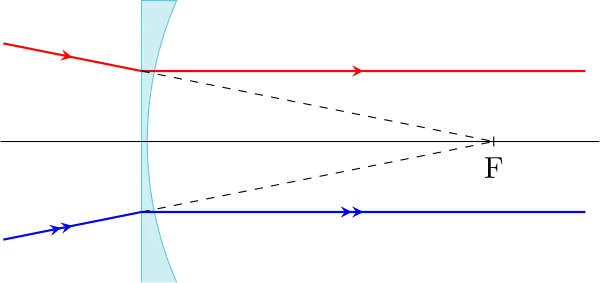
Une lentille divergente comporte aussi deux foyers, dont les positions sont inversées par rapport à ceux de la lentille convergente :
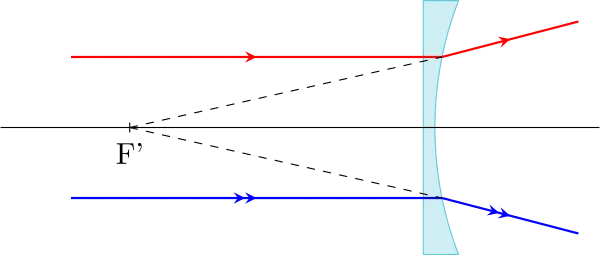
Tout rayon incident dont le prolongement passe par F, foyer principal objet, émerge parallèle à l’axe optique ;
Tout rayon incident parallèle à l’axe optique émerge de façon à ce que leur prolongement passe par F’ ;
Ces foyers sont également symétriques par rapport au centre optique de la lentille.
Distance focale et vergence
A retenir
La distance focale est la grandeur algébrique \(\overline{OF'}\) qui s’exprime en mètre (m). Elle est donc positive pour une lentille convergente mais négative pour une lentille divergente.
La vergence est définie par :
\begin{equation}\boxed{V = \dfrac{1}{\overline{OF'}}}\end{equation}
Elle s’exprime en dioptries (\(\delta\)) ou (\(\mathrm{m}^{-1}\)). Elle est positive dans le cas d’une lentille convergente, négative dans le cas d’une lentille divergente.
Relations de grandissement et de conjugaison
Pour établir celles-ci, nous nous servons de la construction la plus classique de l’image d’un objet AB situé au delà du foyer de la lentille convergente (\(|\overline{OA}| > |\overline{OF}|\)).Mais on notera que ceci est valable quelle que soit la position de l’objet et quelle que soit la nature de la lentille.
Pour effectuer cette construction, on peut tracer trois rayons dont les directions de propagation sont
connues :
Le rayon qui passe par le centre optique de la lentille n’est pas dévié ;
Le rayon qui arrive parallèlement à l’axe optique sur la lentille émerge en passant par F’ ;
Le rayon qui passe par F avant d’intercepter la lentille émerge parallèlement à l’axe optique.
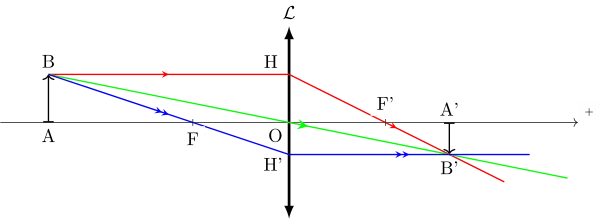
Relations de Newton (origine aux foyers)
En vidéo, la démonstration de ces formules :
D’après le théorème de Thalès appliqué dans les triangles ABF et OH’F :
\begin{equation}\gamma = \dfrac{\overline{A'B'}}{\overline{AB}} = \dfrac{\overline{OH'}}{\overline{AB}} = \dfrac{\overline{FO}}{\overline{FA}}\end{equation}
D’après le théorème de Thalès appliqué dans les triangles HOF’ et F’A’B’ :
\begin{equation}\gamma = \dfrac{\overline{A'B'}}{\overline{AB}} = \dfrac{\overline{A'B'}}{\overline{OH}} = \dfrac{\overline{F'A'}}{\overline{F'O}}\end{equation}
En combinant les deux relations précédentes, on obtient :
\begin{equation}\boxed{\overline{F'A'}\;\overline{FA} = \overline{F'O}\;\overline{FO} = -f'^2}\end{equation}
Relations de Descartes (origine au centre)
En vidéo, la démonstration de ces formules :
Pour obtenir le grandissement, on applique le théorème de Thalès dans les triangles OAB et OA’B’ :
\begin{equation}\gamma = \dfrac{\overline{A'B'}}{\overline{AB}} = \dfrac{\overline{OA'}}{\overline{OA}}\end{equation}
Pour obtenir la relation de conjugaison, on part de la relation de Newton et on introduit le point O :
\begin{equation}(\overline{F'O}+\overline{OA'})(\overline{FO}+\overline{OA})=-f'^2\end{equation}
On remplace \(\overline{F'O}\) par \(-f'\) et \(\overline{FO}\) par f’, on développe, les termes en \(f'^2\) disparaissent. On a :
\begin{equation}f'\;\overline{OA'} - f'\;\overline{OA}+ \overline{OA}\;\overline{OA'} = 0\end{equation}
Et en divisant par \(f'\;\overline{OA}\;\overline{OA'}\), on obtient :
\begin{equation}\boxed{\dfrac{1}{\overline{OA'}}-\dfrac{1}{\overline{OA}}=\dfrac{1}{f'}}\end{equation}
Lentilles accolées
Soient deux lentilles de vergence \(V_1\) et \(V_2\) accolées : on considère leurs centres optiques comme confondus. La première lentille donne une image qui devient l’objet pour la deuxième lentille. L’application de la relation de conjugaison à se système permet de montrer que ce doublet se comporte comme un lentille unique de vergence \(V = V_1 + V_2\). On pourra donc appliquer la relation de conjugaison comme s’il s’agissait une seule lentille.
Attention ! Si les lentilles ne sont pas accolées, la relation de conjugaison n’est plus valable.
Des constructions pour toutes les configurations
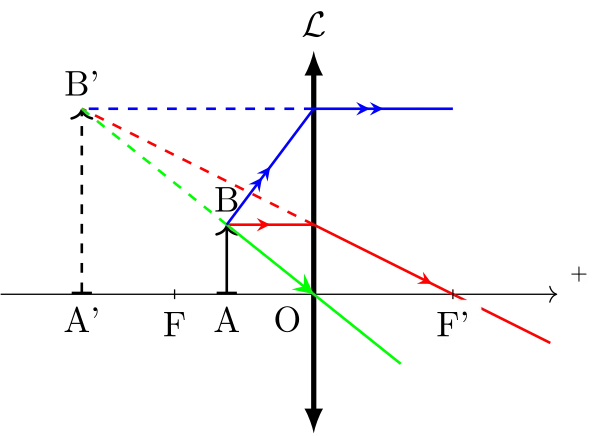
Cas d’une lentille convergente

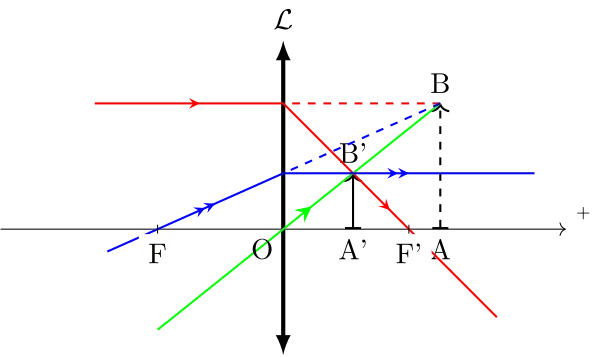
Cas d’une lentille divergente
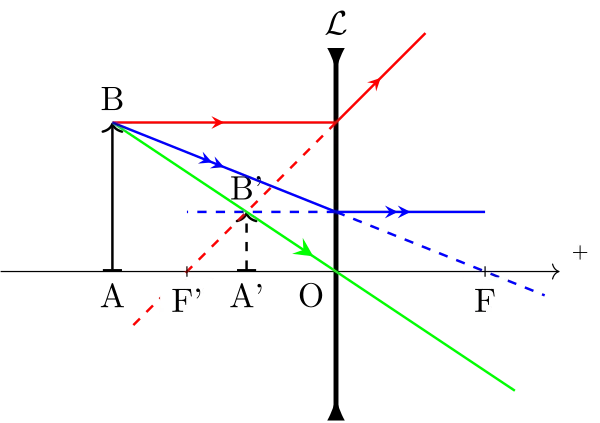
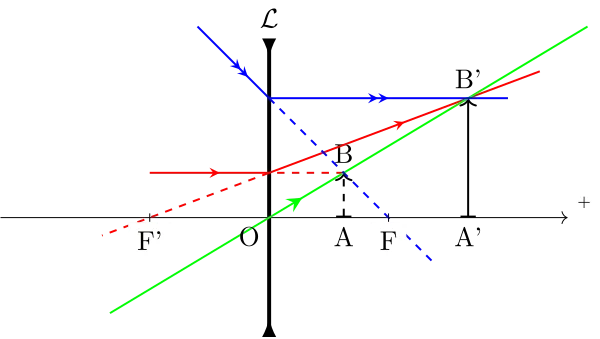
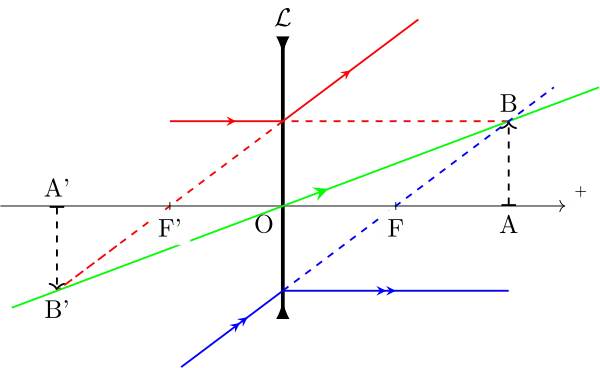
Construction de l’émergent correspondant à un incident donné
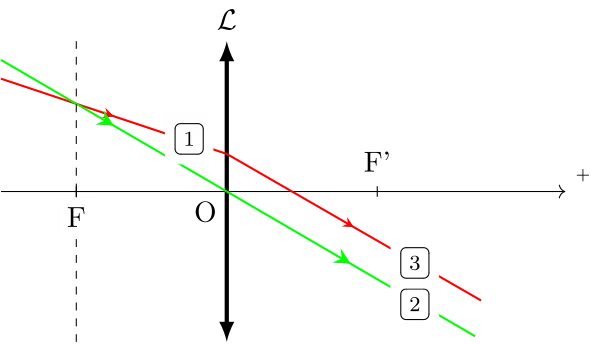
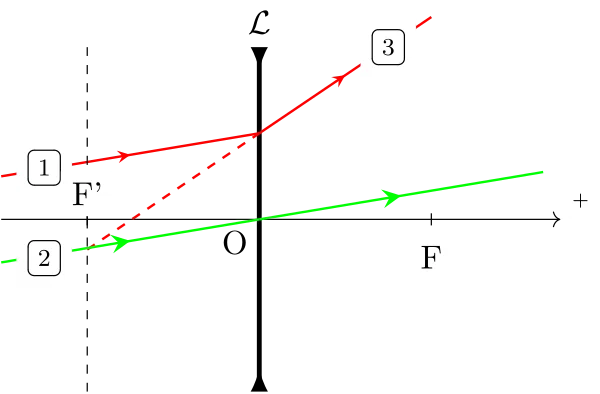
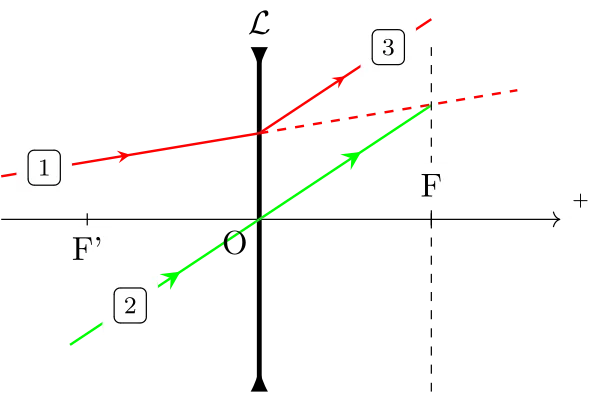
De la même manière que pour les miroirs, on utilise un rayon dont on connaît le parcourt : le rayon qui passe par le centre optique de la lentille, qui n’est pas dévié. Soit on le trace parallèle à l’incident et on sait qu’il croisera l’émergent dans le plan focale image ; soit on le trace croisant l’incident dans le plan focale objet, et on sait qu’il sera parallèle à l’émergent.
En vidéo, une des méthodes de tracé pour la lentille convergente et pour la lentille divergente :
Sinon, voici des constructions qui montrent le principe de ce travail :
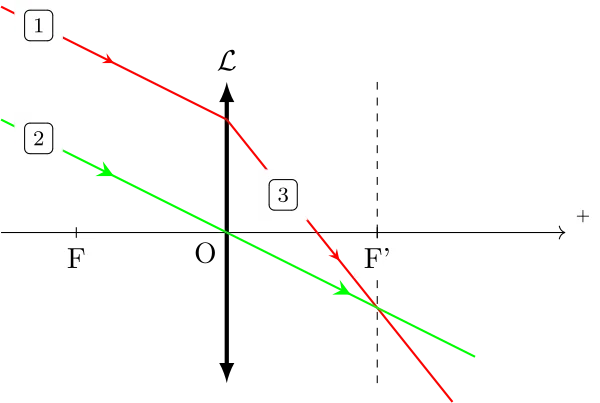
Aberrations des systèmes optiques
On désigne par le terme aberrations les défauts que présente l’image créée par un système optique du fait des écarts aux conditions de Gauss ou à la dispersion. On distingue donc deux types d’aberrations :
Les aberrations chromatiques dues à la dispersion de la lumière blanche ;
Les aberrations géométriques dues aux écarts par rapport aux condition de Gauss.
Aberrations chromatiques
Comme nous l’avons vu dans le premier chapitre de ce cours d’optique les verres sont dispersifs : une radiation bleue sera davantage dévié qu’une radiation rouge. Ainsi, dans les lentilles, le foyer image qui concentre les rayons parallèles à l’axe optique, a une position différente suivant la couleur de la lumière. La focale des lentilles est donc légèrement différentes suivant la couleur.
Il en résulte des images irisées puisque l’image finale est composée d’images superposées de différentes couleurs.Pour corriger ce défaut, qui n’affecte que les systèmes réfracteurs (lentilles et non miroirs), on fabrique des associations de lentilles (convergente et divergente) dont les effets chromatiques se compensent.
Aberration de sphéricité
Nous l’avons déjà rencontré dans le cas des miroirs, elle existe aussi dans le cas des lentilles : cette aberration provient de la différence de convergence des rayons qui frappent la lentille (ou le miroir) loin ou près de son axe optique.
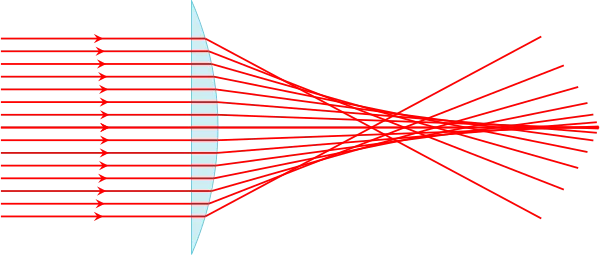
Pour corriger cette aberration, il paraît logique de placer un diaphragme sur le système et de le fermer suffisamment. Mais il en résulte une perte de luminosité. Ainsi, comme pour les aberrations chromatiques, on cherche une association de lentilles (convergente et divergente) dont les effets de sphéricité se compensent.
La distorsion
Cette aberration intervient lorsque l’on cherche à faire l’image d’un objet transverse de grande taille. On est alors amené à utiliser un diaphragme afin que la lentille soit utilisée dans les conditions de Gauss. Mais la position du diaphragme est très importante sous peine d’obtenir une image distordue :
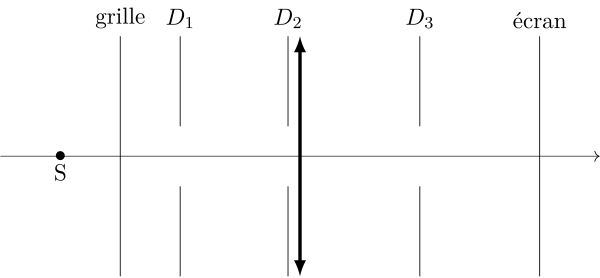
En pointillés est schématisée l’image que l’on attend.
Si le diaphragme est situé loin en avant de la lentille (position \(\text{D}_1\)), les rayons marginaux sont les seuls à passer par le diaphragme et donnent un point image qui s’écarte de l’axe optique par rapport à la position attendue. Et inversement si le diaphragme est situé loin en arrière de la lentille (position \(\text{D}_3\)).
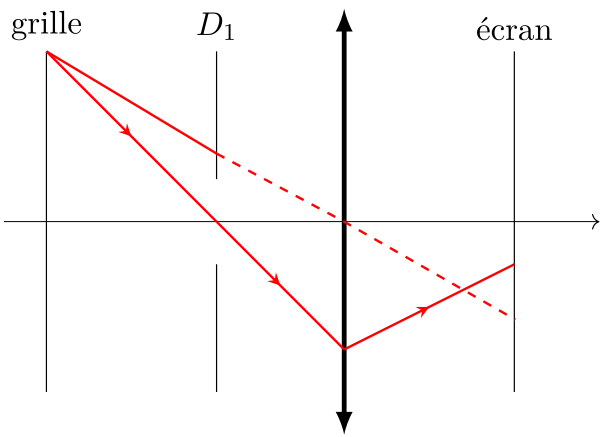
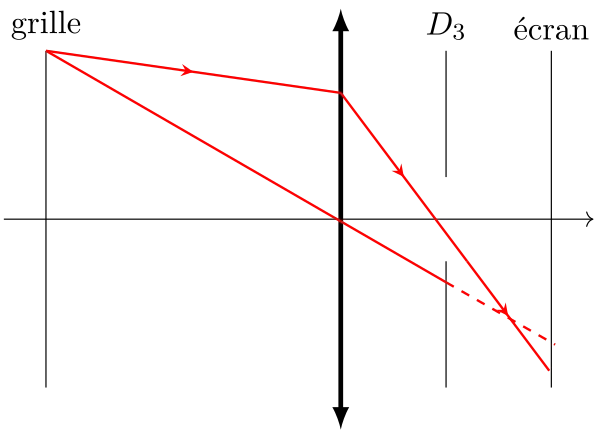
La seule bonne position pour le diaphragme est celle où il est accolé à la lentille (position \(\text{D}_2\)), aucune distorsion n’apparaît.
Références
- "Physique Tout-en-un MPSI PCSI PTSI" - Marie-Noëlle Sanz / Anne-Emmanuelle Badel / François Clausset - Editions Dunod 2008 ;
- "Précis Optique MPSI PCSI PTSI" - P.Brenders / M.Sauzeix - Bréal ;
- Cours sur les lentilles par Jimmy Roussel


