Licence 1 > Optique 1 > Cours sur les généralités sur les systèmes optiques et les miroirs
02 : généralités sur les systèmes optiques, miroirs sphériques
Introduction
Nous allons dans ce deuxième chapitre étudié la propagation de la lumière à travers un système optique. Après avoir défini ce qu’est un système optique, on commencera à parler d’objets et d’images ce qui nous permettra de définir les notions de stigmatisme, d’aplanétisme. En lien avec ces deux notions, on étudiera les miroirs.
Généralités sur les systèmes optiques
Sources de lumière
On pourra rencontrer en optique plusieurs types de sources lumineuses que l’on caractérise comme ceci :
les sources isotropes, qui émettent de la lumière dans toutes les directions ;
Les sources anisotropes, qui émettent de la lumière dans une portion limitée d’espace ;
Les sources à l’infini, qui sont si loin que leurs rayons nous arrivent parallèles.
Système optique
Un système optique (S) est un ensemble de milieux transparents séparés par des dioptres ou des miroirs. Citons quelques qualificatifs possibles pour ces systèmes :
Un système est dioptrique s’il ne comporte que des dioptres ;
Le système le plus général étant le catadioptrique, mélange de dioptres et de miroirs.
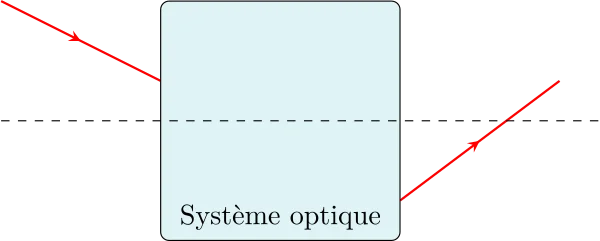
Le système optique (S) sera représenté par un espace coloré, avec sa face d’entrée dans lequel pénètre un rayon incident et sa face de sortie de laquelle sort un rayon émergent. Le système est centré sur un axe appelé axe optique.La lumière se propage conventionnellement de la gauche vers la droite.
Stigmatisme, objets et images
Stigmatisme
A retenir
Un système optique est rigoureusement stigmatique si tous les rayons émis par A, point objet, convergent en un seul point A’, appelé point image. On dit que A et A’ sont conjugués par le système optique.
Images réelle et virtuelle
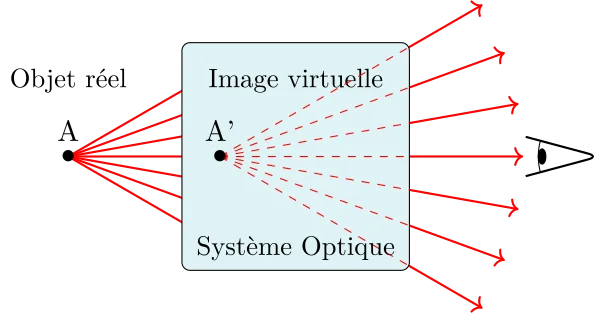
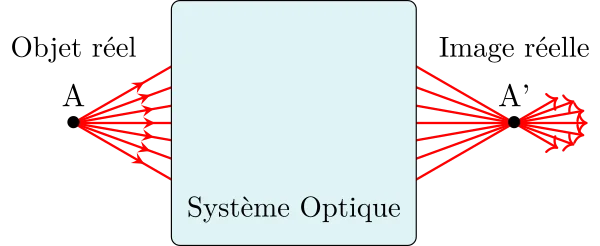
Soit un point objet A émettant des rayons lumineux vers le système optique. Deux cas peuvent se présenter :
Les rayons émergent du système optique en convergeant vers un point A’ : ce point est un point image réel, on peut le recueillir sur un écran ;
Les rayons émergent du système optique en divergeant mais leurs prolongements se coupe en un point A’ : ce point est un point image virtuel, on ne peut pas le recueillir sur un écran mais il peut être vu à l’œil nu à travers le système.
Remarque
En effet, l’œil reçoit des rayons lumineux provenant d’un même point, celui-ci joue le rôle d’objet pour la lentille de l’œil et une image se forme sur la rétine.
Objets réel et virtuel
De façon identique à ce qui a été dit précédemment, on peut créer un point objet virtuel en faisant converger les prolongements de rayons incidents au système optique. L’image de ce point objet virtuel pourra être un point image réel ou un point image virtuel selon les même principes énoncés au paragraphe précédent.
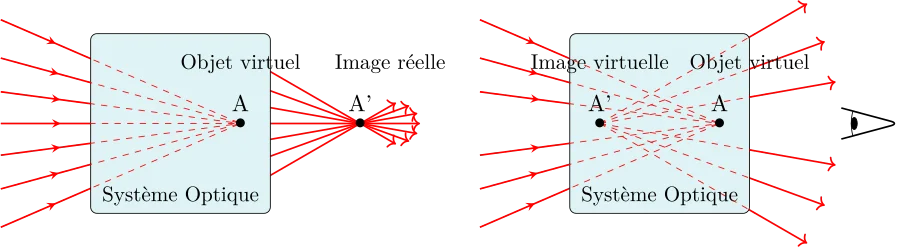
Espaces objet et image
Autour d’un système optique s’organise alors quatre espaces :
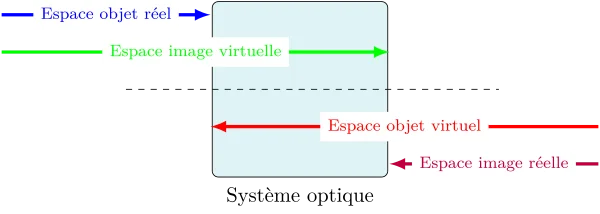
Foyers
Les foyers d’un système optique sont des points particuliers :
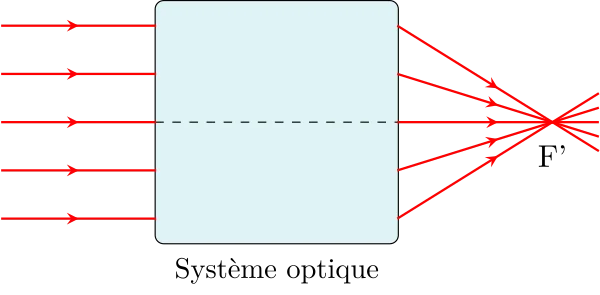
Le foyer principal image F’ est le point image d’un objet situé à l’infini, dont les rayons arrivent parallèles sur le système optique et parallèlement à son axe optique. Le plan passant par F’ et perpendiculaire à l’axe optique du système est appelé plan focal image.
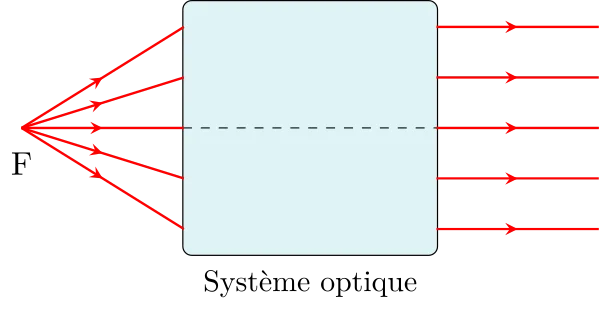
Le foyer principal objet F est le point objet d’une image située à l’infini, les rayons émergent du système optique parallèles entre eux et parallèles à l’axe optique. Le plan passant par F et perpendiculaire à l’axe optique du système est appelé plan focal objet.
Remarque Des rayons parallèles mais inclinés par rapport à l’axe optique se croisent en un point du plan focal image, appelé foyer secondaire image. De même avec un point du plan focal objet ...
Aplanétisme
A retenir
Soit A et A’, et B et B’, deux couples de points conjugués par le système optique (S). B est situé dans le plan transverse (le plan perpendiculaire à l’axe optique du système) de A.Si B’ est situé dans le plan transverse de B, alors le système est rigoureusement aplanétique.
Les miroirs
Le miroir plan
Un système rigoureux
A retenir
Le miroir plan est le seul système optique rigoureusement stigmatique et aplanétique.
Construction de l’image d’un point objet
Les rayons issus du point objet A entrent dans le système optique, émergent alors des rayons qui soit se coupent directement pour donner un point image réel, soit leurs prolongements se coupent pour donner un point image virtuel.
Pour construire l’image A’ de A, on utilise deux rayons incidents et on applique les lois de la réflexion :
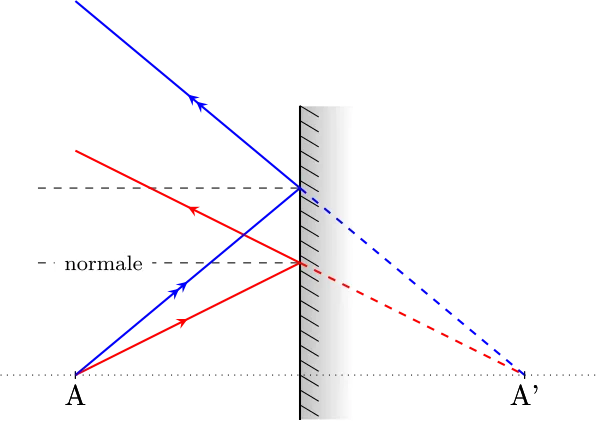
A retenir
Ainsi, le point image A’ est le symétrique du point objet A par rapport au plan du miroir.La relation de conjugaison du miroir plan s’écrit :
\begin{equation}\overline{HA}=-\overline{HA'}\end{equation}
où H est le projeté orthogonal de A sur le miroir plan.
Cette image est une image virtuelle puisqu’elle est le point d’intersection de prolongement de rayons émergents. Seul un œil bien placé permettra de voir cette image.
Peut-on obtenir une image réelle avec un miroir plan ? Oui ! il suffit d’utiliser le principe de retour inverse de la lumière sur la figure 8 : on fait converger des rayons dans le miroir pour créer un objet virtuel qui donne alors une image réelle que l’on peut recueillir sur un écran.
Applications : grandissement transverse et axial
Questions
Construire l’image d’un segment AB transverse (parallèle au miroir), calculer le grandissement transverse défini par \(\gamma_t = \dfrac{\overline{A'B'}}{\overline{AB}}\)
Construire l’image d’un segment AB axial (perpendiculaire au miroir), calculer le grandissement axial défini par \(\gamma_a = \dfrac{\overline{A'B'}}{\overline{AB}}\)
Réponses
Construction
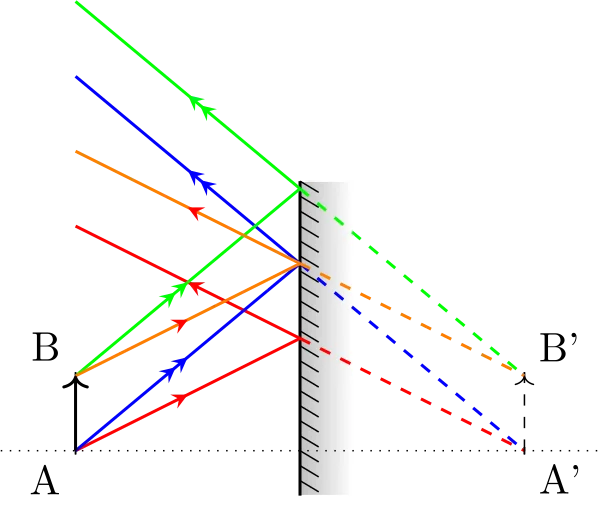
Image d'un objet transverse Le grandissement transversal est de 1 : image droite et pas de déformation. Par contre, il y inversion gauche droite entre l’objet et l’image.
Construction
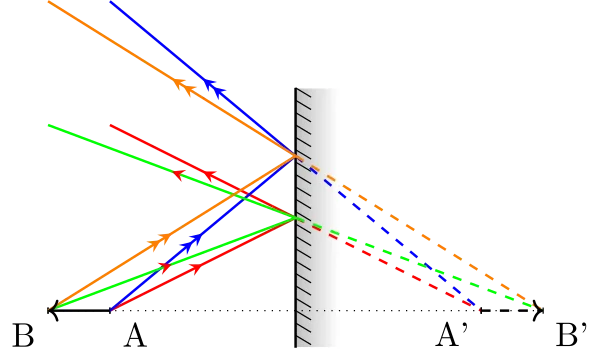
Image d'un objet axial Le grandissement axial est de -1 : image renversée et toujours pas de déformation.
Le miroir sphérique
Deux types de miroirs
Définitions
A retenir
Un miroir sphérique est une portion de sphère réfléchissante. Deux cas peuvent alors se présenter :
Voici la représentation des miroirs et leur caractère convergent ou divergent :
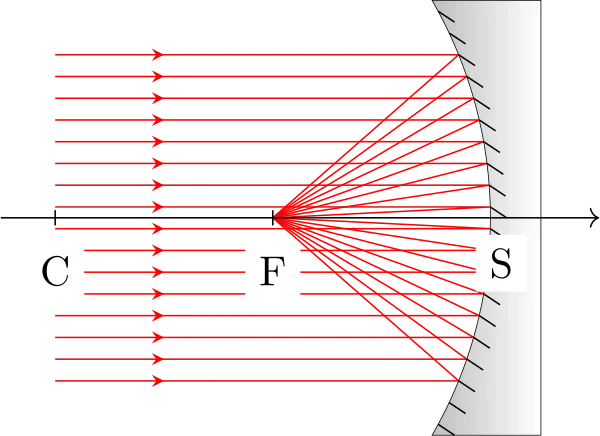
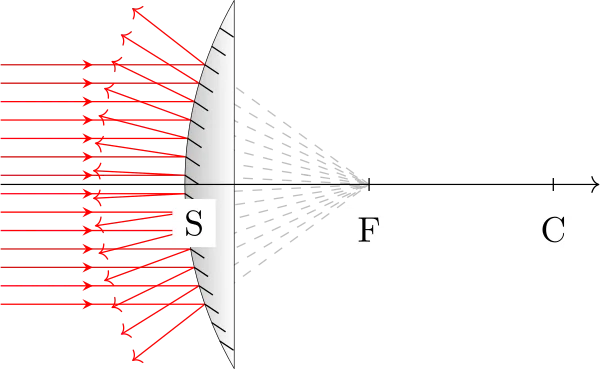
Points particuliers
A retenir
On appelle C le centre du miroir : il s’agit du centre de la sphère réfléchissante dont une partie constitue le miroir ; un rayon qui passe par C n’est pas dévié ;
On appelle S le sommet du miroir : c’est le point d’intersection entre l’axe optique et la surface réfléchissante.
Attention, les figures [concave] et [convexe] montrent des miroirs stigmatiques (ils ne le sont qu’à certaines conditions, voir paragraphe suivant).Alors dans ce cas, on peut définir :
A retenir
Le foyer du miroir, car foyer principal image et foyer principal objet sont confondus : les rayons qui arrivent sur le miroir parallèlement à l’axe optique se coupent en F ; et inversement, les rayons qui passent par F et frappent le miroir se réfléchissent parallèlement à l’axe optique.
Dans le cas du miroir stigmatique, le foyer F se situe au milieu de SC.
Le foyer F est réel dans le cas d’un miroir concave, virtuel dans le cas d’un miroir convexe.
La distance focale du miroir est définie par \(f=\overline{SF}=\dfrac{\overline{SC}}{2}\). Elle s’exprime en mètre (\(\mathrm{m}\)).Cette distance focale est négative dans le cas d’un miroir concave, positive dans le cas d’un miroir convexe.
La vergence du miroir est définie par \(V = \dfrac{1}{\overline{SF}}\). Elle s’exprime en dioptrie (symbole \(\delta\)) ou \(\mathrm{m^{-1}}\).Cette vergence est donc négative dans le cas d’un miroir concave, positive dans le cas d’un miroir convexe.
Remarque On définit aussi souvent le rayon algébrique du miroir : \(R = \overline{CS}\).
Le miroir concave et le stigmatisme
Le miroir concave n’est pas rigoureusement stigmatique : en effet, en considérant des rayons parallèles frappant le miroir en des points d’incidence éloignés du sommet S, on remarque que l’image du point objet situé à l’infini n’est plus un point : les rayons ne convergent plus en un seul point F.
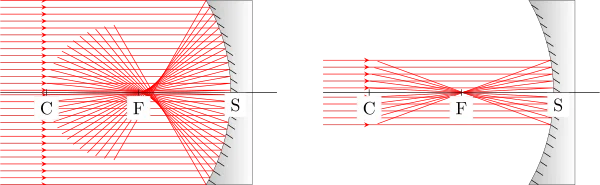
Pour avoir une image ponctuelle, il ne faut considérer que les rayons proches du sommet S du miroir, on les appelle des rayons paraxiaux. Dans ce cas, c’est comme si les rayons frappait un miroir plan puisque la courbure est peu prononcée entre les deux rayons paraxiaux extrêmes.
Mais ceci n’est pas suffisant, on peut montrer qu’il faut également que les rayons ne soient pas trop inclinés par rapport à l’axe optique du miroir.
Ainsi pour qu’un miroir sphérique soit stigmatique, il faut respecter certaines conditions appelées conditions de Gauss.
Le miroir concave et l’aplanétisme
Si le miroir sphérique n’est pas stigmatique, il ne peut pas être aplanétique. Mais on montre que s’il est stigmatique approché, il sera également aplanétique approché (l’image A’B’ d’un objet transverse AB est transverse) si les conditions de Gauss sont respectées.
Les conditions de Gauss
A retenir
Pour qu’un système optique soit stigmatique et aplanétique approchés, il faut l’utiliser dans les conditions de Gauss :
Les rayons doivent être paraxiaux (l’angle que chacun fait avec l’axe optique du système doit être petit) ;
Les rayons doivent rencontrer la surface du système proche de leur sommet situé sur l’axe optique ;
Ces deux conditions impliquent que les angles d’incidence des rayons sont petits.
Démonstration
On peut montrer mathématiquement que l’approximation de stigmatisme approché n’est valable que si les rayons sont paraxiaux. Pour se faire, on montre que la position de F est déterminée à cette condition.
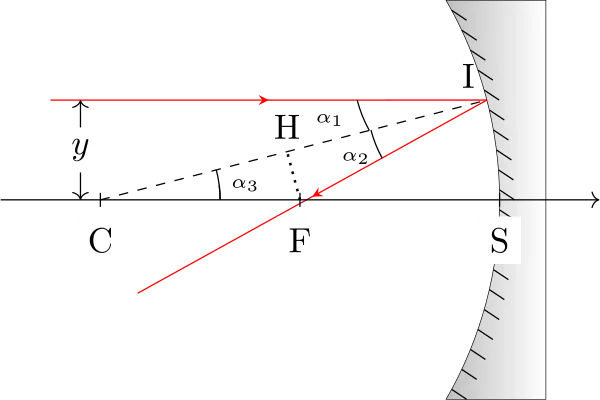
A condition que y soit petit :
Le triangle CIF est isocèle : en effet, \(\alpha_1\) = \(\alpha_2\) grâce aux lois de la réflexion, et \(\alpha_1\) = \(\alpha_3\) car le même segment (en pointillés) coupe deux droites parallèles.On a donc \(\alpha_2\) = \(\alpha_3\).
Si on trace le projeté orthogonal H de F sur CI, on a \(CH \simeq \dfrac{R}{2}\) (si y est petit) ; et on peut écrire dans le triangle CHF :
\begin{equation}\cos \alpha = \dfrac{CH}{CF} = \dfrac{\frac{R}{2}}{CF}\end{equation}
On peut exprimer \(\alpha\) en fonction de \(y\) et de \(R\) :
\begin{equation}\sin \alpha = \dfrac{y}{R}\end{equation}
Enfin on sait que \(\cos^2 + \sin^2 = 1\), on peut donc obtenir :
\begin{equation}\boxed{CF = \dfrac{\frac{R}{2}}{\cos \alpha} = \dfrac{\frac{R}{2}}{\sqrt{1-\left(\dfrac{y}{R}\right)^2}}}\end{equation}
Même avec un \(y\) petit, CF dépend bien a priori de cette hauteur du rayon (\(y\)).Ce ne sera plus le cas lorsque y << R \(\left(\text{alors } CF = \dfrac{R}{2}\right)\), ce qui correspond à la condition d’avoir des rayons paraxiaux.
Formules de conjugaison
Pour établir celles-ci, nous nous servons de la construction la plus classique de l’image d’un objet AB situé au delà du centre du miroir concave (\(|\overline{SA}| > |\overline{SC}|\)). Mais on notera que ceci est valable quelle que soit la position de l’objet et quelle que soit la nature du miroir.
Pour effectuer cette construction, on peut tracer quatre rayons dont les directions de propagation sont connues :
Le rayon qui arrive parallèle sur le miroir est réfléchi en passant par le foyer ;
Le rayon qui passe par le foyer se réfléchit dans le miroir en étant parallèle à l’axe optique ;
Le rayon qui passe par C et qui se réfléchit dans le miroir n’est pas dévié (il a la direction de la normale).
Le rayon qui frappe le miroir en son sommet est réfléchi avec un angle de réflexion identique à son angle d’incidence.
On obtient alors la construction suivante :
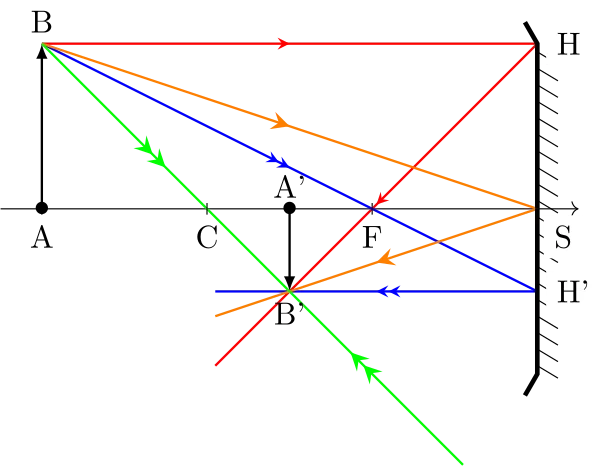
Formules de Newton
Ces formules sont appelés relations avec origine aux foyers.
Le théorème de Thalès va nous permettre de les établir.Dans les triangles BAF et FSH’, on a :
\begin{equation}\gamma = \dfrac{\overline{A'B'}}{\overline{AB}}=\dfrac{\overline{SH'}}{\overline{AB}}=\dfrac{\overline{FS}}{\overline{FA}}\end{equation}
On obtient une première relation définissant le grandissement par rapport à la position de l’objet. Dans les triangles B’A’F et FSH, on a :
\begin{equation}\gamma = \dfrac{\overline{A'B'}}{\overline{AB}}=\dfrac{\overline{A'B'}}{\overline{SH}}=\dfrac{\overline{FA'}}{\overline{FS}}\end{equation}
On obtient ici une deuxième relation définissant le grandissement par rapport à la position de l’image cette fois-ci.
En combinant ces deux relations, on peut établir la relation de Newton :
\begin{equation}\boxed{\overline{FA}\overline{FA'}=\overline{FS}^2=f^2=ff'}\end{equation}
Formules avec origine au centre
En utilisant le théorème de Thalès dans les triangles CAB et CA’B’, on établit une nouvelle expression du grandissement :
\begin{equation}\gamma=\dfrac{\overline{A'B'}}{\overline{AB}}=\dfrac{\overline{CA'}}{\overline{CA}}\end{equation}
En partant de la relation de Newton et en introduisant le centre C du miroir, on établit la relation de conjugaison avec origine au centre :
\begin{equation}(\overline{FC}+\overline{CA})(\overline{FC}+\overline{CA'})=f^2\end{equation}
Or \(\overline{FC}=f\) :
\begin{equation}f^2+f \overline{CA}+f \overline{CA'}+\overline{CA} \overline{CA'}=f^2\end{equation}
On divise par \(f\,\overline{CA}\,\overline{CA'}\) :
\begin{equation}\dfrac{1}{\overline{CA'}}+\dfrac{1}{\overline{CA}}=-\dfrac{1}{f}\end{equation}
Enfin, \(f=\dfrac{\overline{SC}}{2}\) :
\begin{equation}\boxed{\dfrac{1}{\overline{CA'}}+\dfrac{1}{\overline{CA}}=\dfrac{2}{\overline{CS}}}\end{equation}
Formules avec origine au sommet
Le théorème de Thalès appliqué aux triangles SAB et SA’B’ permet d’écrire une relation de grandissement :
\begin{equation}\gamma=\dfrac{\overline{A'B'}}{\overline{AB}}=-\dfrac{\overline{SA'}}{\overline{SA}}\end{equation}
Pour la relation de conjugaison, on part toujours de la relation de Newton et on introduit le point S :
\begin{equation}(\overline{FS}+\overline{SA})(\overline{FS}+\overline{SA'})=f^2\end{equation}
Or \(\overline{FS}=-f\), on peut développer :
\begin{equation}f^2-f \overline{SA}-f \overline{SA'}+\overline{SA} \overline{SA'}=f^2\end{equation}
On divise par \(f\,\overline{SA}\,\overline{SA'}\) :
\begin{equation}\dfrac{1}{\overline{SA'}}+\dfrac{1}{\overline{SA}}=\dfrac{1}{f}\end{equation}
Enfin, \(f=\dfrac{\overline{SC}}{2}\) :
\begin{equation}\boxed{\dfrac{1}{\overline{SA'}}+\dfrac{1}{\overline{SA}}=\dfrac{2}{\overline{SC}}}\end{equation}
Des constructions pour toutes les configurations
Miroir concave
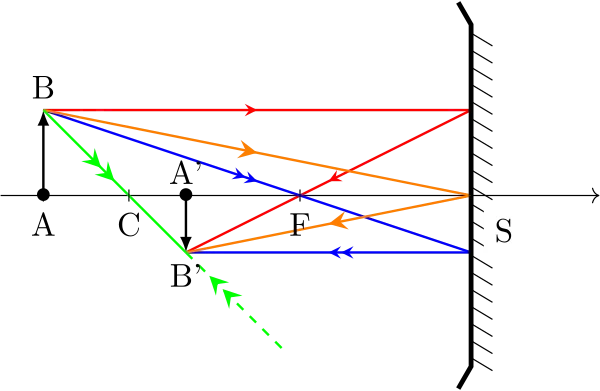
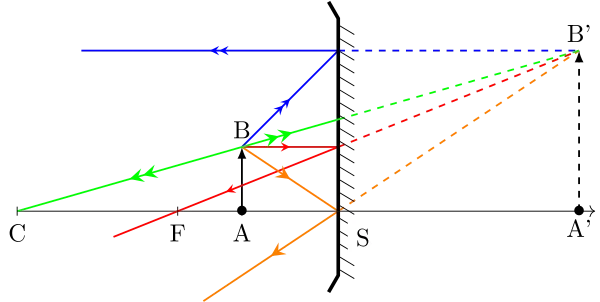
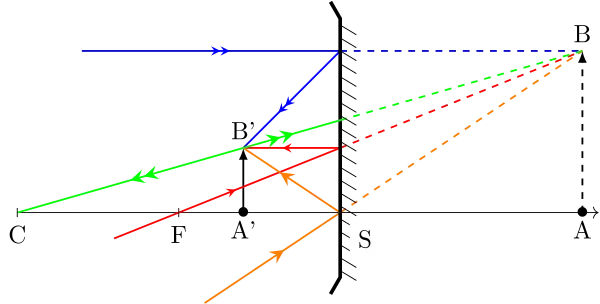
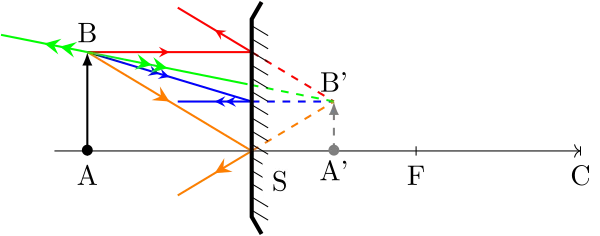
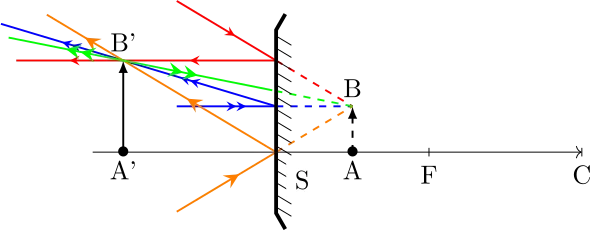
Miroir convexe
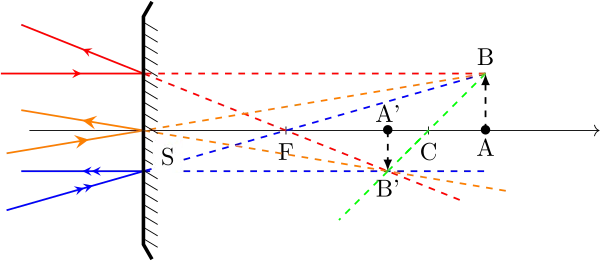
Construction d’un rayon réfléchi correspondant à un incident donné
Il faut utiliser un rayon dont on connaît le parcourt qui est parallèle au rayon incident ou à l’émergent recherché.En effet, nous savons que des rayons incidents parallèles donnent des émergents qui se croisent dans le plan focale image ; et à des incidents qui se croisent dans le plan focal objet correspondent des émergents qui sont parallèles.
Voici deux exemples de constructions pour un miroir concave :
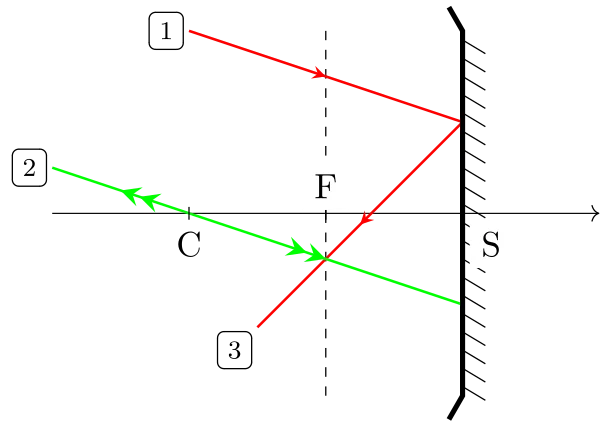
Construction de l’émergent d’un incident quelconque : utilisation d’un foyer secondaire image
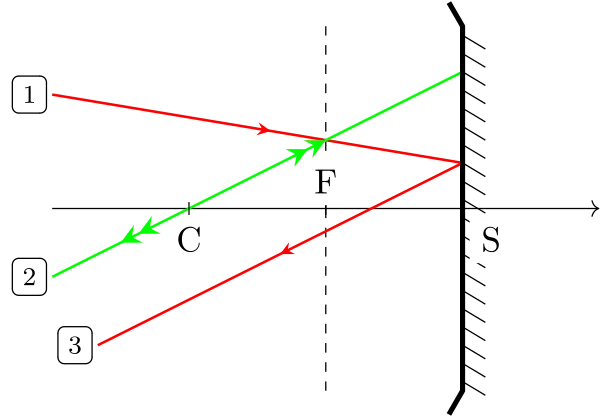
Construction de l’émergent d’un incident quelconque : utilisation d’un foyer secondaire objet
Voici deux exemples de constructions pour un miroir convexe :
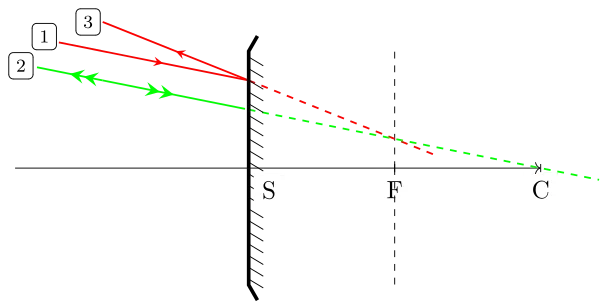
Construction de l’émergent d’un incident quelconque : utilisation d’un foyer secondaire image
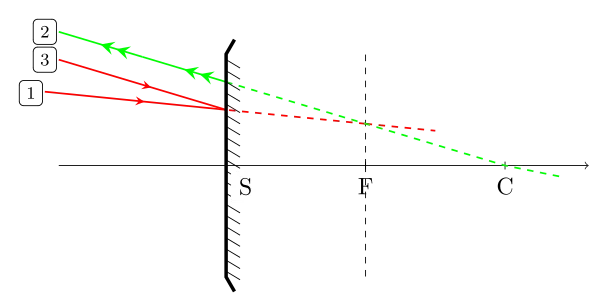
Construction de l’émergent d’un incident quelconque : utilisation d’un foyer secondaire objet
Références
- "Physique Tout-en-un MPSI PCSI PTSI" - Marie-Noëlle Sanz / Anne-Emmanuelle Badel / François Clausset - Editions Dunod 2008 ;
- "Précis Optique MPSI PCSI PTSI - P.Brenders / M.Sauzeix - Bréal ;
- Cours sur les systèmes optiques et les miroirs par Jimmy Roussel


