Licence 1 > électrocinétique > Résumé de cours : EC4 : régime sinusoïdal
EC4 : régime sinusoïdal
L'essentiel
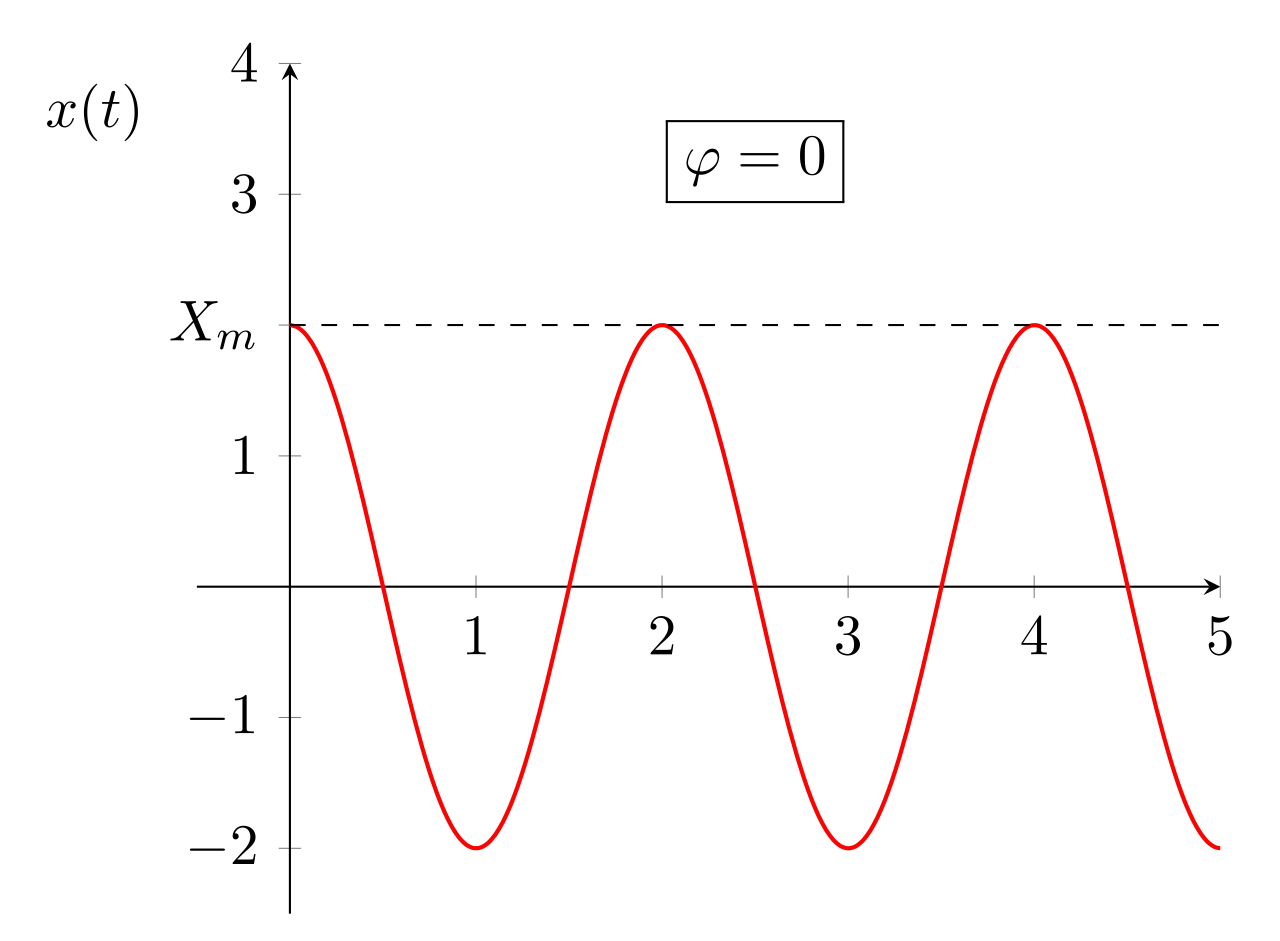
Forme graphique et mathématiques d’une grandeur sinusoïdale
\begin{equation}\boxed{x(t)=X_m\cos (\omega t + \phi)}\end{equation}
où \(X_m\) est l’amplitude, \(\omega\) la pulsation et \(\phi\) la phase à l’origine de la grandeur.
Relations entre la pulsation, la période et la fréquence
\begin{equation}\boxed{\omega = \frac{2\pi}{T}} \hspace{2cm} \boxed{\omega=2\pi f} \hspace{2cm} \boxed{f=\frac{1}{T}}\end{equation}
Déphasage entre deux signaux
On considère toujours le déphasage entre deux signaux synchrones, c’est à dire de même fréquence.
Ce déphasage varie entre \(0\) et \(\pi\) et peut être positif ou négatif.
Si on considère par exemple le déphasage de \(V_S\) par rapport à \(V_E\) :
- Le déphasage est positif si \(V_S\) est en avance par rapport à \(V_E\) (sur un oscillogramme \(V=f(t)\), le tracé représentant \(V_S\) commence celui avant \(V_E\));
- Le déphasage est négatif si \(V_S\) est en avance par rapport à \(V_E\).
Forme complexe d’un signal sinusoïdal
Soit un signal sinusoïdal d’expression mathématique \(x(t)=X_m\cos (\omega t + \phi)\), on lui associe une grandeur complexe :
\begin{equation}\boxed{\underline{x}(t) = X_m e^{j(\omega t + \phi)} = X_m e^{j\omega t} e^{j\phi}}\end{equation}
On définira également une amplitude complexe :
\begin{equation}\boxed{\underline{X}=X_m e^{j\phi}} \hspace{0.5cm} \text{donc} \hspace{0.5cm} \boxed{\underline{x}(t) = \underline{X}e^{j\omega t}}\end{equation}
Lien entre grandeur complexe et grandeurs réelles
Pour retourner au signal réel complet :
\begin{equation}\boxed{x(t) = Re(\underline{x}(t))}\end{equation}
Retour à l’amplitude du signal réel :
\begin{equation}\boxed{X_m = |\underline{X}| = |\underline{x}(t)|}\end{equation}
Retour à la phase initiale :
\begin{equation}\boxed{\phi = Arg(\underline{X})}\end{equation}
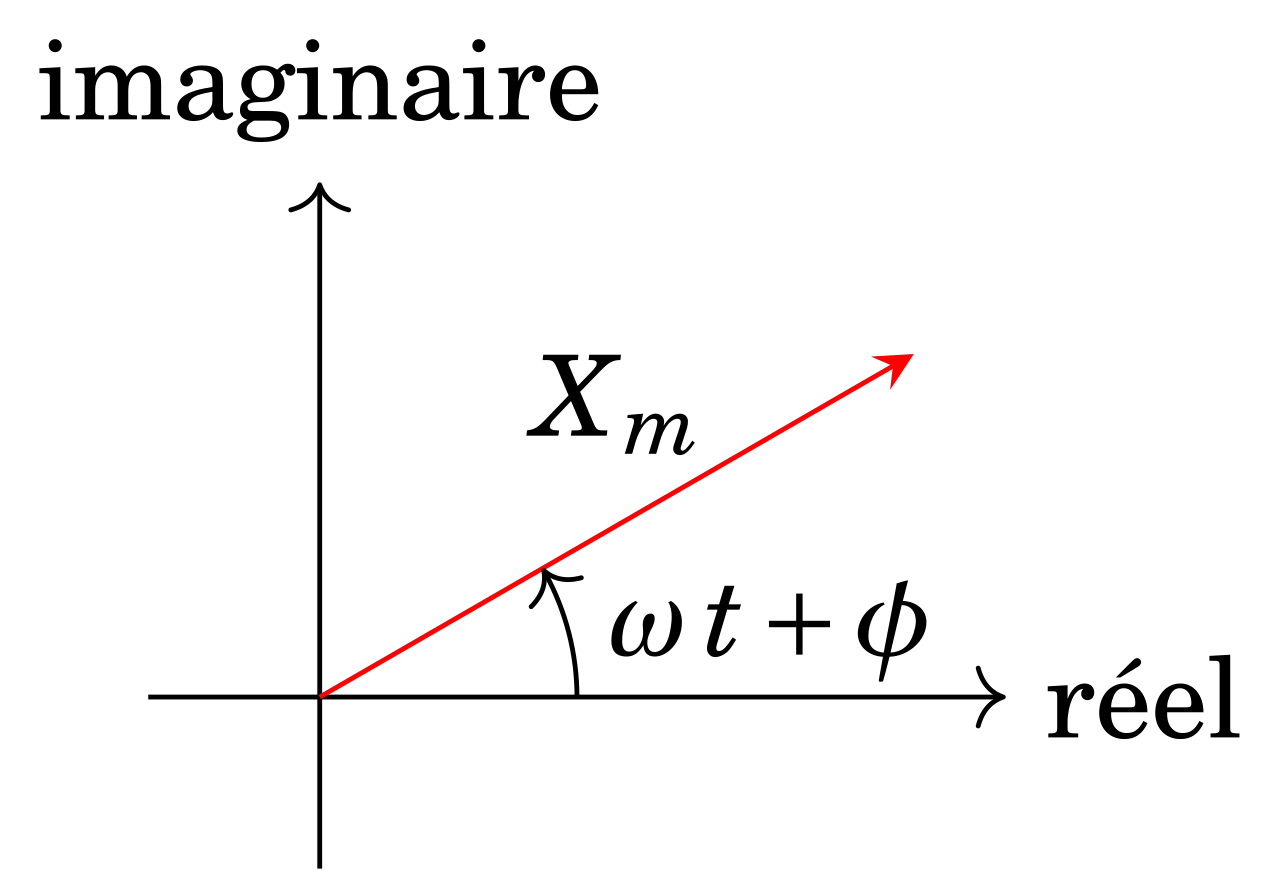
Représentation de Fresnel
Dérivation de signaux complexes
\begin{equation}\boxed{\dfrac{d\underline{x}(t)}{dt}=j\omega \underline{x}(t)}\end{equation}
Intégration de signaux complexes
\begin{equation}\boxed{\int \underline{x}(t) = \dfrac{1}{j\omega} \underline{x}(t) }\end{equation}
Notation complexe et régime forcé : étude du dipôle RC
On cherche \(u(t)\) aux bornes du condensateur.On peut écrire la loi des mailles en notation complexe :
\begin{equation}\boxed{\underline{u}(t) + R\,\underline{i}(t) = E e^{j(\omega t)}}\end{equation}
Or \(i(t) = C\dfrac{du(t)}{dt}\) donc \(\underline{i}(t) = C\dfrac{d\underline{u}(t)}{dt} = jC\omega \underline{u}(t)\) (la relation entre \(\underline{i}(t)\) et \(\underline{u}(t)\) est linéaire).
Elle devient simplement :
\begin{equation}\boxed{\underline{u}(t) = \dfrac{E e^{j(\omega t)}}{1+jRC\omega}}\end{equation}
Intérêt des complexes : il n’y a plus d’équation différentielle à résoudre.
On obtient l’amplitude de \(u(t)\) en calculant le module de \(\underline{U}\) :
\begin{equation}\boxed{U = |\underline{U}|=\dfrac{E}{\sqrt{1+\tau^2\omega^2}}}\end{equation}
Et la phase à l’origine de \(u(t)\) en prenant l’argument \(\underline{U}\) :Attention, pour obtenir cette phase, il faut calculer la tangente et connaître le signe du cosinus.On obtient :
\begin{equation}\boxed{\tan \phi = - \tau\omega}\end{equation}
et
\begin{equation}\boxed{\cos \phi = \dfrac{\dfrac{E}{1+(\tau\omega)^2}}{|\underline{U}|} > 0}\end{equation}
Donc on peut écrire :
\begin{equation}\boxed{\phi = \arctan(-\tau\omega)}\end{equation}
Finalement :
\begin{equation}\boxed{u(t) = \dfrac{E}{\sqrt{1+R^2C^2\omega^2}} \cos(\omega t - \arctan (\tau\omega))}\end{equation}
Impédance et Admittance complexe
Impédance complexe :
\begin{equation}\boxed{\underline{Z} = \dfrac{\underline{u}}{\underline{i}}}\end{equation}
Admittance complexe :
\begin{equation}\boxed{\underline{Y} =\dfrac{1}{\underline{Z}} = \dfrac{\underline{i}}{\underline{u}}}\end{equation}
Impédance des dipôles linéaires
Résistance :
\begin{equation}\boxed{\underline{Z} = R}\end{equation}
Condensateur :
\begin{equation}\boxed{\underline{Z} = \dfrac{1}{jC\omega}}\end{equation}
Le condensateur se comporte en basses fréquences comme un interrupteur ouvert, en hautes fréquences comme un interrupteur fermé. Bobine :
\begin{equation}\boxed{\underline{Z} = jL\omega}\end{equation}
La bobine se comporte en basses fréquences comme un interrupteur fermé, en hautes fréquences comme un interrupteur ouvert.
Loi d’ohm en notation complexe
\begin{equation}\boxed{\underline{u}=\underline{Z}\times\underline{i}}\end{equation}
Impédance complexe et grandeurs réelles
- Le module de l’impédance complexe donne le rapport de l’amplitude de la tension par l’amplitude de l’intensité ;
- L’argument de l’impédance complexe donne le déphasage (avance de phase) entre la tension u(t) et l’intensité i(t).
Condensateur, bobine et déphasage
- Une bobine introduit un déphasage de \(\pi/2\) entre la tension et l’intensité ;
- Un condensateur introduit un déphasage de \(-\pi/2\) entre la tension et l’intensité.
Lois en notation complexe
Les lois vues dans le chapitre EC1 sont valables pour les grandeurs complexes : association d’impédances, loi des noeuds, loi des mailles, ponts diviseurs, ...
Valeur efficace d’un signal
Pour un signal quelconque :
\begin{equation}X_\mathrm{eff}^2 = <x(t)^2> = \dfrac{1}{T}\int_0^T x^2(t) dt\end{equation}
Dans le cas d’une grandeur sinusoïdale :
\begin{equation}\boxed{X_{\mathrm{eff}}=\frac{X_\mathrm{m}}{\sqrt{2}}}\end{equation}
Puissance instantanée
La formule générale est :
\begin{equation}\boxed{p(t)=u(t)\times i(t)}\end{equation}
Si \(u(t) = U_m \cos(\omega t + \phi)\) et \(i(t) = I_m \cos(\omega t + \phi')\) :
\begin{equation}p(t) = \dfrac{U_\mathrm{m}I_\mathrm{m}}{2}\left(\cos(2\omega t + \phi + \phi')+\cos(\phi-\phi')\right)\end{equation}
Puissance moyenne
\begin{equation}P = \dfrac{1}{T}\int_0^T p(t) dt\end{equation}
\begin{equation}\boxed{P = \dfrac{U_\mathrm{m}I_\mathrm{m}}{2} \cos \Delta\phi = U_{\mathrm{eff}}I_{\mathrm{eff}} \cos \Delta\phi}\end{equation}
Le terme \(\cos \Delta\phi\) est appelé facteur de puissance.


