Licence 1 > Electrocinétique 1 > Résumé de cours sur les lois de l'électrocinétique dans l'ARQS

EC1 : lois dans l'approximation des régimes quasi-stationnaires
L'essentiel

Electrocinétique

L’électrocinétique est l’étude du mouvement d’ensemble des porteurs de charges dans un circuit que l’on appelle courant électrique.

Intensité du courant

C’est une grandeur algébrique.
Comme nous l’avons déjà vu, l’intensité du courant est la quantité de charges \(\delta q\) qui traverse une section S du conducteur pendant un temps \(\delta t\). Son unité est l’ampère (A), \(1\,\mathrm{A}\) correspond à \(1\,\mathrm{C.s^{-1}}\).

Tension électrique

La tension est une différence de potentiel électrique entre deux points d’un circuit et se mesure avec un voltmètre qui la donne en Volt (V).

5 On note \(U_{AB} = V(A)-V(B)\) par une flèche dirigée de A vers B. \(U_{AB}\) est positive si \(V(A)>V(B)\).

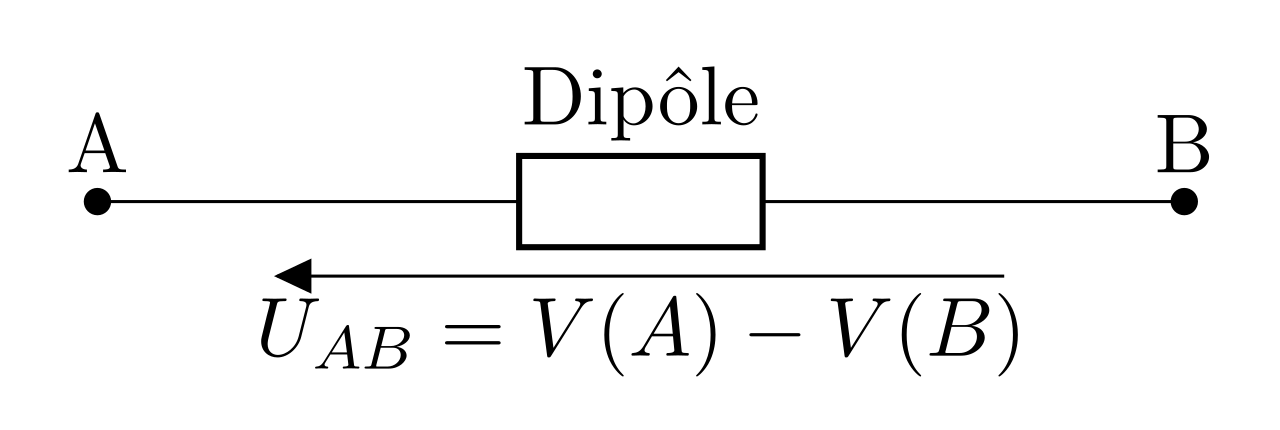
Approximation des régimes quasi-stationnaires (ARQS)

Cette approximation consiste à dire que quel que soit le régime (continu ou variable), l’intensité du courant est la même en tout point d’une branche.

Loi des mailles

La somme des tensions à l’intérieur d’une maille est nulle. Sur la maille ABCD, on a :

\begin{equation*}\boxed{U_{AB} + U_{BC} + U_{CD} + U_{DA} = 0 \nonumber }\end{equation*}

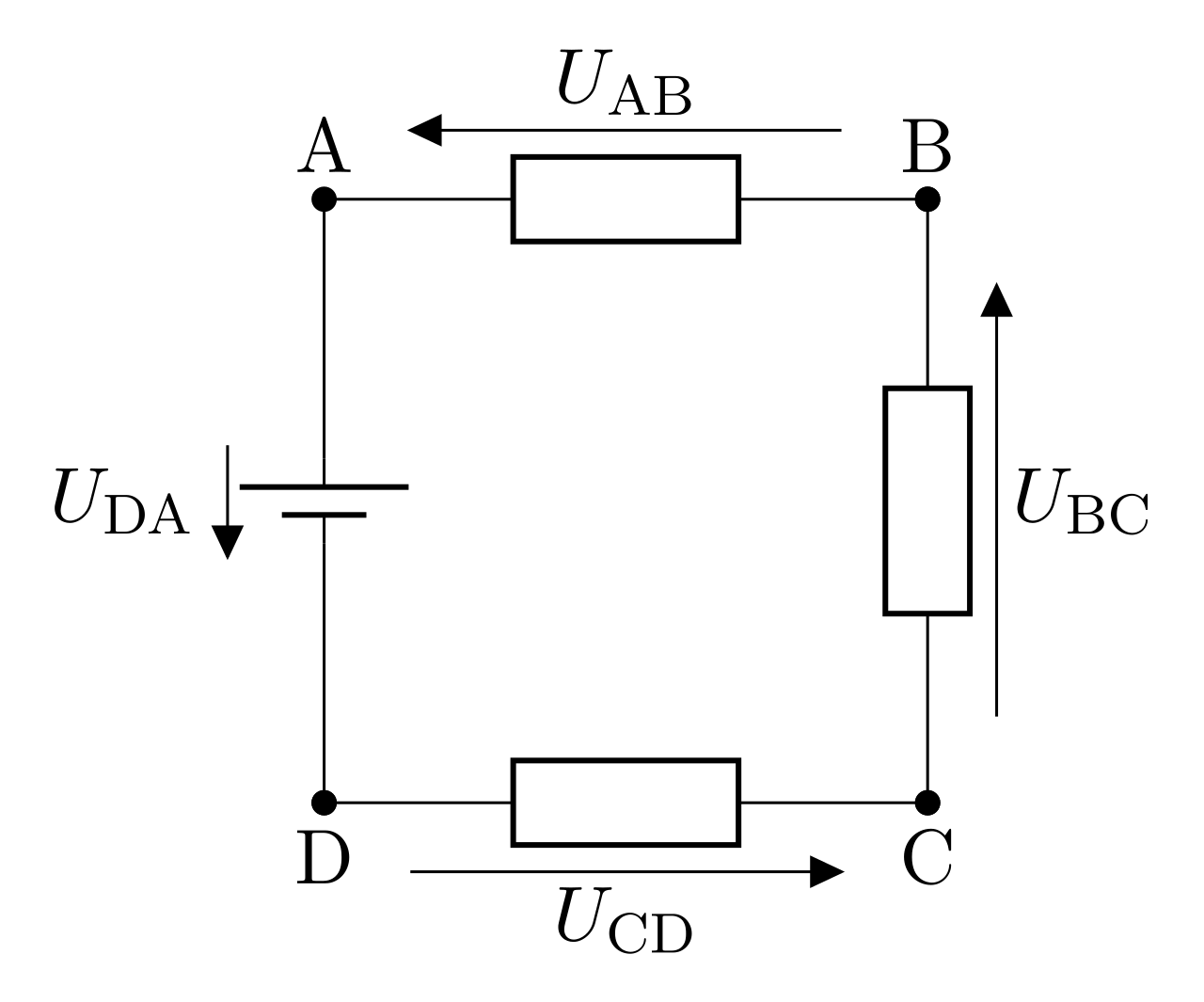
Loi des nœuds

La somme des courants qui arrivent sur un noeud est égale à la somme des courants qui en repart :

\begin{equation*}\boxed{I_1 = I_2 + I_3 \nonumber }\end{equation*}

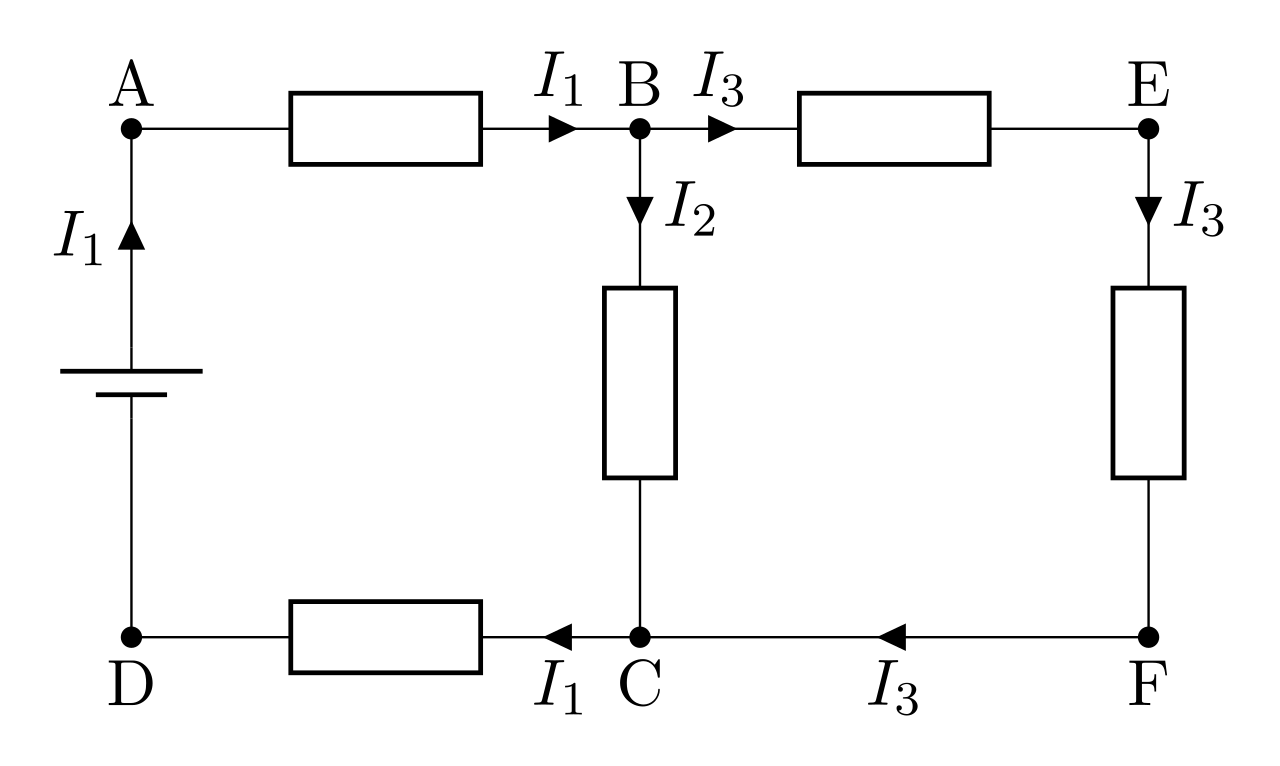
Puissance reçue et convention

La puissance reçue par un dipôle est définie par :

\begin{equation*}\boxed{P=U\times I} \nonumber\end{equation*}

Comme la puissance reçue est positive pour un récepteur, la définition ci-dessous s’écrit pour la convention récepteur :

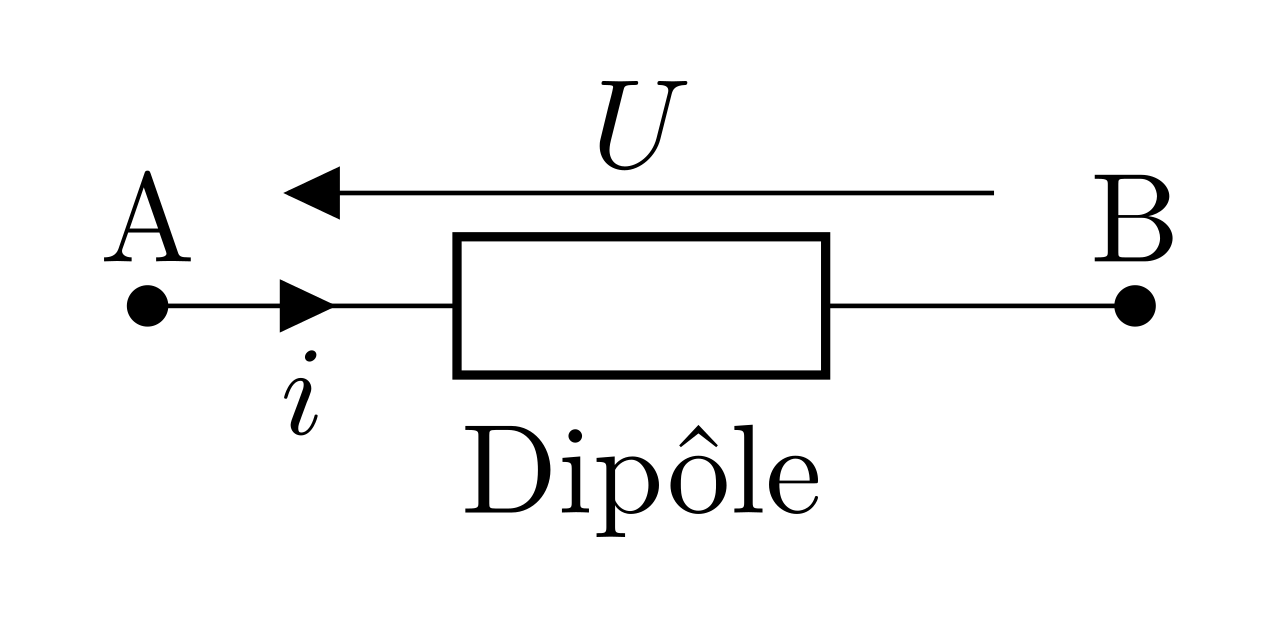
Pour un dipôle générateur, la puissance reçue est négative et on schématise le dipôle en convention générateur :

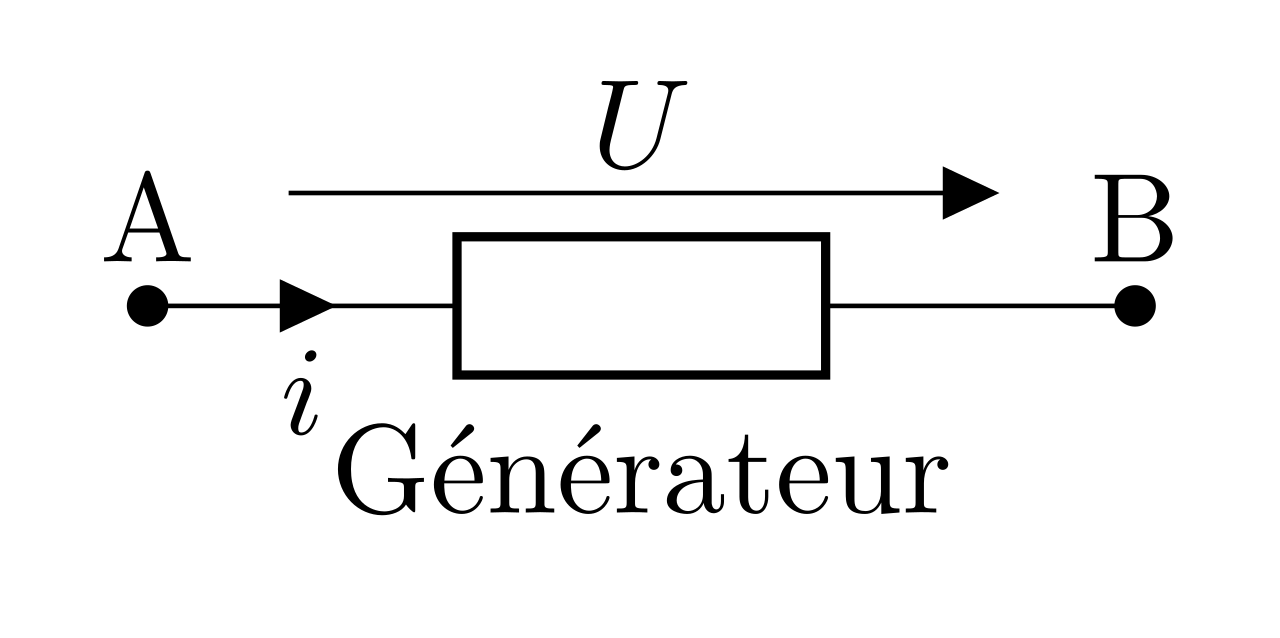
Caractéristique d’un dipôle

La caractéristique tension-courant d’un dipôle est la fonction \(u=f(i)\).

Dipôle actif ou passif

Un dipôle passif est un dipôle qui convertit toute l’énergie électrique qu’il reçoit en énergie thermique (conducteur ohmique, diode, ...).
Sa caractéristique passera forcément par l’origine.

Un dipôle actif fournit à l’extérieur de l’énergie thermique et une autre forme d’énergie

Loi d’Ohm pour un conducteur ohmique

Un conducteur ohmique est un dipôle dont la caractéristique est une droite passant par l’origine. Il répond donc à la loi d’Ohm qui s’écrit :

\begin{equation*}\boxed{u=Ri} \nonumber\end{equation*}

Effet Joule

Le conducteur ohmique reçoit de l’énergie électrique qu’il dissipe entièrement sous forme de chaleur : c’est l’effet Joule. La puissance dissipée par effet Joule vaut :

\begin{equation*}\boxed{P=Ri^{2}} \nonumber\end{equation*}

Association de conducteurs ohmiques en série

0 Pour la situation ci-contre, on a :

\begin{equation*}\boxed{R_{\mathrm{eq}}=R_{1}+R_{2}+R_{3}} \nonumber\end{equation*}

Montage diviseur de tension

\begin{equation*}\boxed{U_{R_1} = \dfrac{R_1}{R_1+R_2}E = \dfrac{R_1}{R_{\mathrm{eq}}}E} \nonumber\end{equation*}

\begin{equation*}\boxed{U_{R_2} = \dfrac{R_2}{R_1+R_2}E = \dfrac{R_2}{R_{\mathrm{eq}}}E} \nonumber\end{equation*}

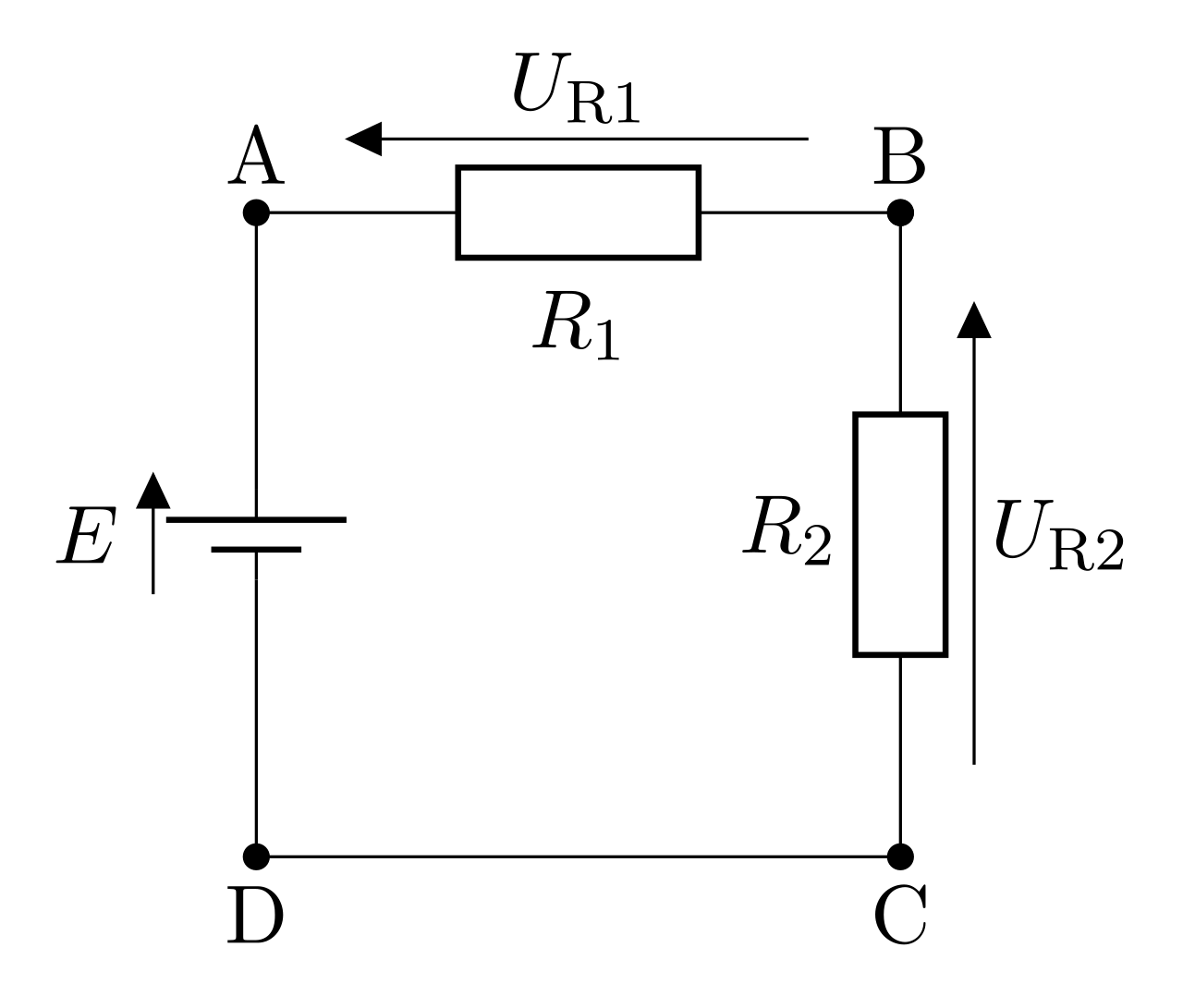
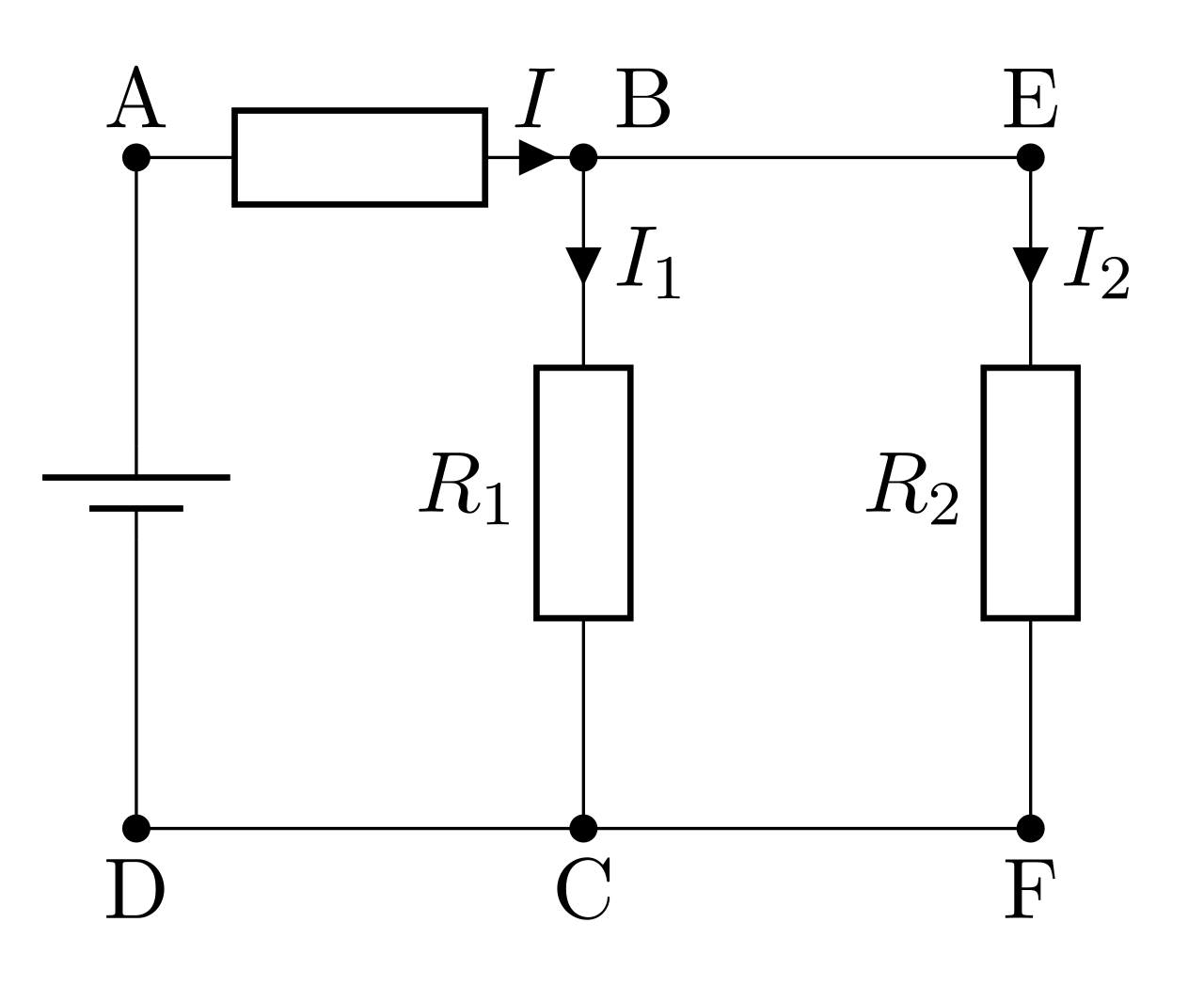
Association de conducteurs ohmiques en parallèles

Pour la situation ci-contre, on a :

\begin{equation*}\boxed{\dfrac{1}{R_{\mathrm{eq}}}= \dfrac{1}{R_{1}} + \dfrac{1}{R_{2}} + \dfrac{1}{R_{3}}} \nonumber\end{equation*}

\begin{equation*}\boxed{G_{\mathrm{eq}}= G_{1} + G_{2} + G_{3}} \nonumber\end{equation*}

Montage diviseur de courant

\begin{equation*}\boxed{I_1 = \dfrac{G_1}{G_1+G_2}I = \dfrac{G_1}{G_{\mathrm{eq}}}I=\dfrac{R_2}{R_1+R_2}I} \nonumber\end{equation*}

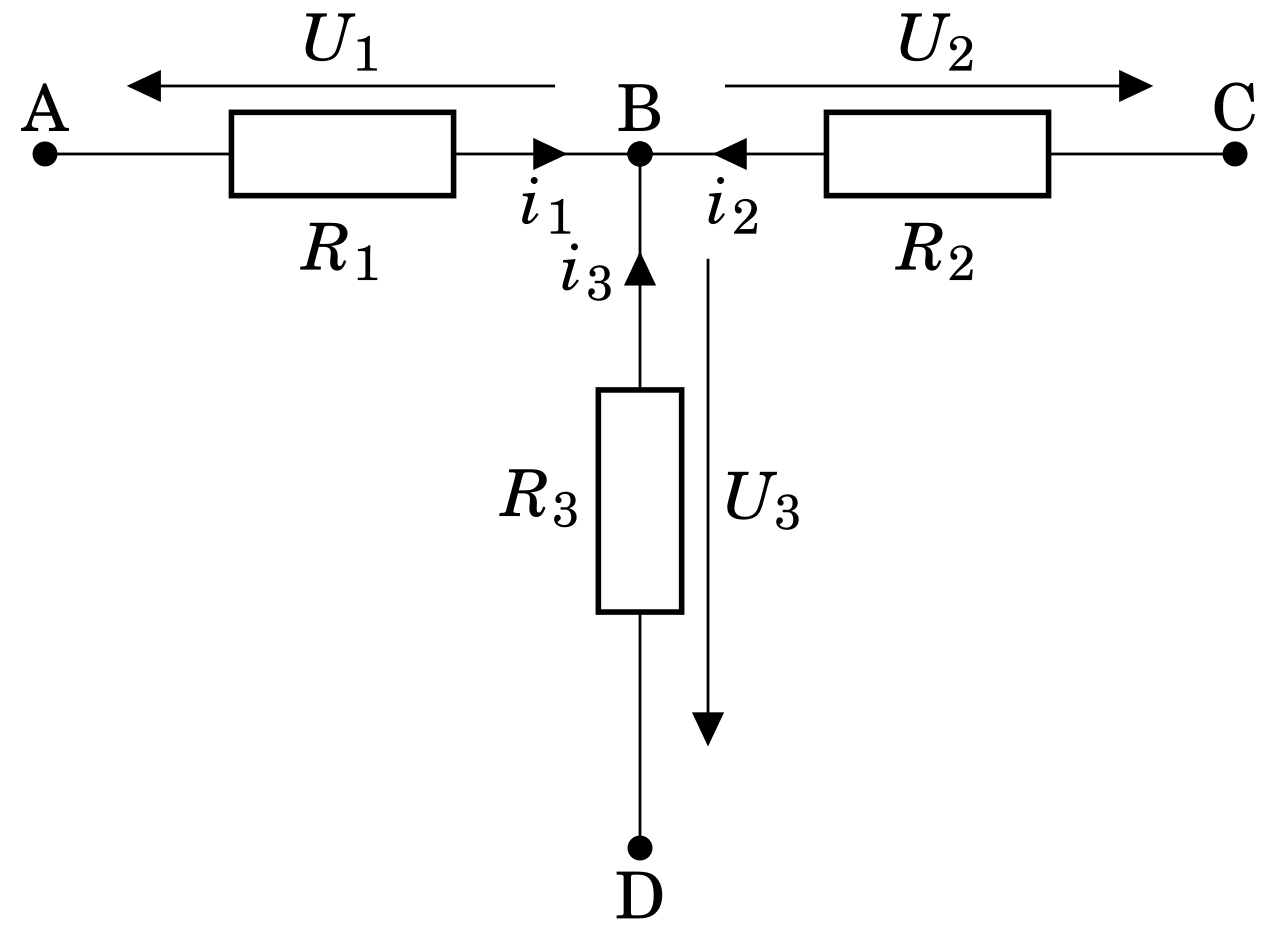
Théorème de Millman

\begin{equation*}\boxed{V_B \left(\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}\right) = \dfrac{V_A}{R_1} + \dfrac{V_C}{R_2} + \dfrac{V_D}{R_3}} \nonumber\end{equation*}

Générateur de tension idéal

Un générateur de tension idéal est un générateur qui délivre une tension constante quel que soit l’intensité débitée.
La tension délivrée est appelée force électromotrice, elle est notée E et s’exprime en Volt (V).

Générateur de courant idéal

Un générateur de courant idéal est un générateur qui délivre une intensité constante quel que soit la tension à ses bornes.
Le courant délivrée est appelée courant électromoteur, il est notée \(\eta\) et s’exprime en Ampère (A).

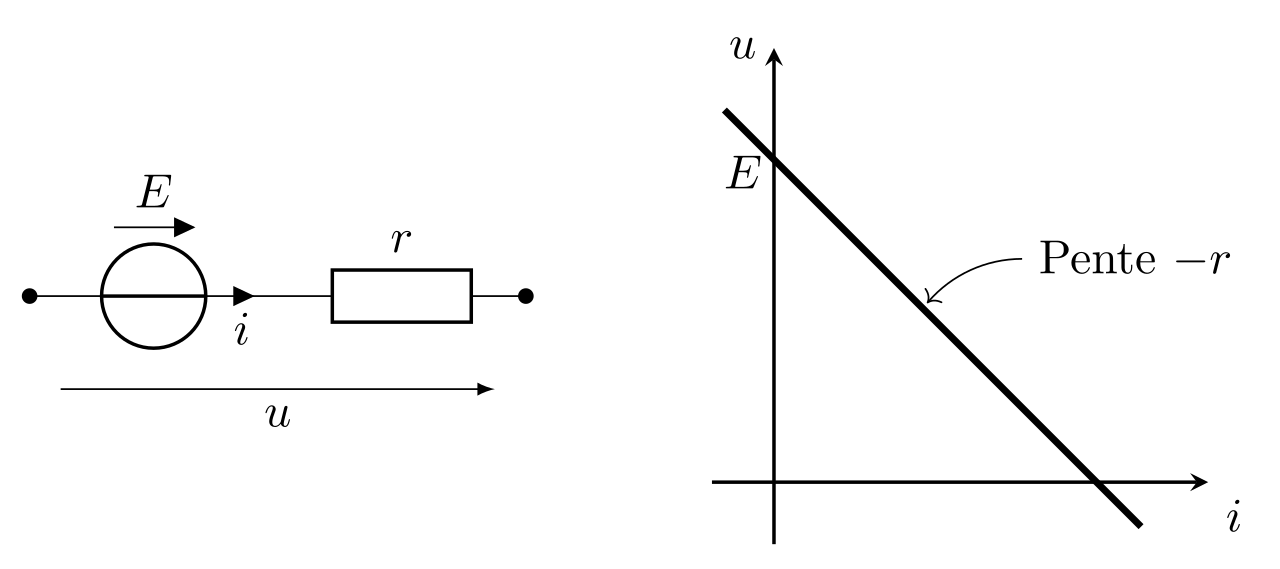
Modèle de Thévenin

Tout générateur réel peut être modélisé par un générateur idéal de tension de fém \(E\) en série avec une résistance \(r\) appelée résistance interne du générateur et exprimée en Ohm (\(\Omega\)).

Sa caractéristique a pour équation :

\begin{equation*}\boxed{u=E-r\times i} \nonumber\end{equation*}

Association

Si deux générateurs de Thévenin (\(E_1\),\(r_1\)) et (\(E_2\),\(r_2\)) sont associés en série, l’ensemble est équivalent à un générateur de Thévenin de fém \(E_1+E_2\) et de résistance interne \(r_1+r_2\).

Modèle de Norton

Tout générateur réel peut être modélisé par un générateur idéal de courant de c.e.m \(\eta\) en parallèle avec une résistance \(r\) appelée résistance interne du générateur et exprimée en Ohm (\(\Omega\)).
On peut aussi introduire \(g\), conductance interne du générateur exprimée en Siemens (S).

Sa caractéristique a pour équation :

\begin{equation*}\boxed{i=\eta - g\times u = \eta-\dfrac{u}{r}} \nonumber\end{equation*}

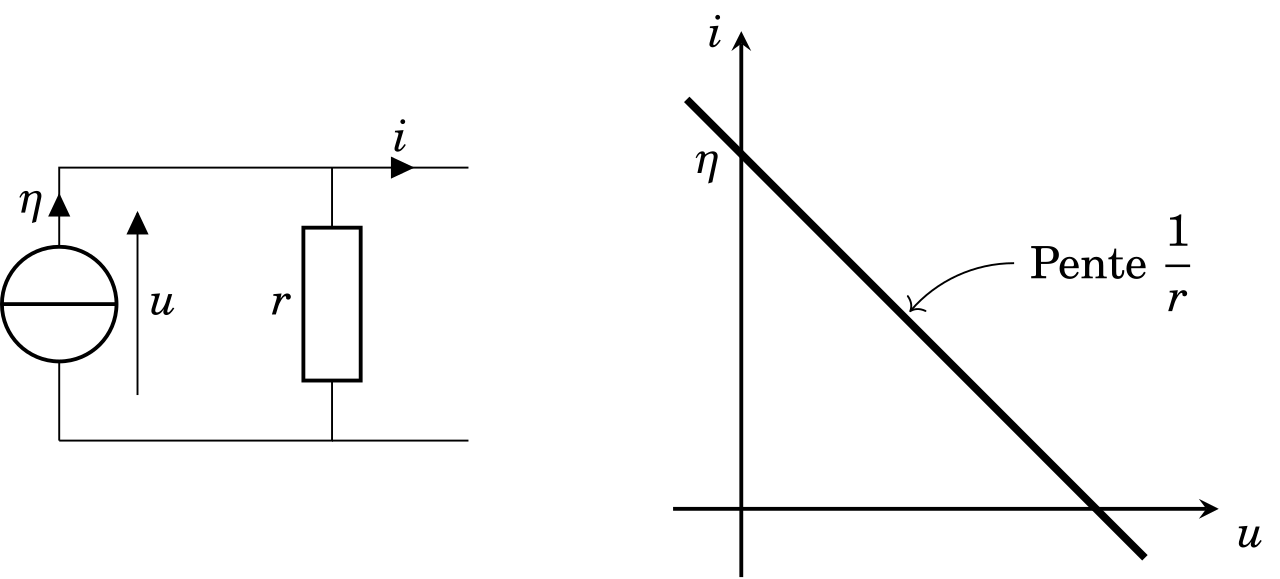
Attention, ici c’est une caractéristique intensité-tension qui est représentée.

Association

Si deux générateurs de Norton identiques (\(\eta_1\),\(g_1\)) et (\(\eta_2\),\(g_2\)) sont associés en parallèle, l’ensemble est équivalent à un générateur de Norton de cém \(\eta_1+\eta_2\) et de conductance interne \(g_1+g_2\).

Passage d’un modèle à l’autre

Les modèles de Thévenin et de Norton sont équivalents, on peut passer de l’un à l’autre à l’aide de la relation :

\begin{equation*}\boxed{E=r\,\eta} \nonumber\end{equation*}