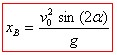Collège/lycée > Fiche ts bac > fiche-ts-bac-physique-11-mouvement-dans-champ-pesanteur-uniforme

Mouvement dans une champ de pesanteur uniforme

Pour un objet dense, profilé, en chute sur quelques mètres, on peut supposer en première approximation que seul le poids s'applique à l'objet : on parlera alors de chute libre.

Equation différentielle du mouvement :

Référentiel galiléen.

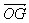 : vecteur position associé au centre d'inertie du système.

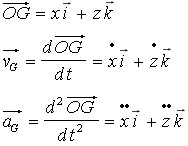
C'est-à-dire : 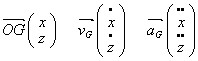 De plus, on a :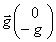  

Or 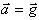  , donc on obtient le système d'équation suivant :

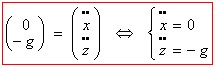
Résolution de l'équation :

Détermination du vecteur vitesse :

Conditions initiales : A t = 0, x₀ = z₀ = 0  

A t = 0, on considère :

Pour obtenir les coordonnées du vecteur vitesse, on cherche une primitive pour chacune des composantes du système écrit ci-dessus :

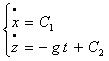
Pour déterminer les constantes, on utilise les conditions initiales :

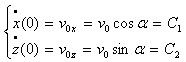
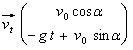
Equation horaire du mouvement :

Pour obtenir les équations horaires du mouvement, il faut calculer une primitive de chacune des composantes de la vitesse :

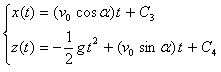
Pour déterminer les constantes, on utilise les conditions initiales :

A t = 0, x(0) = z(0) = C₃ = C₄

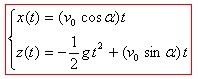
Equation cartésienne de la trajectoire :

On a alors

On introduit cette expression dans z(t) :

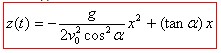
Cette équation est l'équation d'une parabole.

Flèche et portée :

La trajectoire entre le point de départ et la cible est caractérisée par deux grandeurs : la flèche H et la portée D :

La flèche est l'altitude de H la plus élevée atteinte par le projectile. On observe en ce point que la vitesse n'a qu'une composante horizontale donc

d'où - g t_A + v₀ sin α = 0 et (abscisse de A)

On recherche maintenant l'ordonnée de A :

On alors :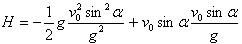 

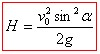
La portée est la distance maximale parcourue par le projectile et est caractérisée par le point d'impact B où z_B = 0

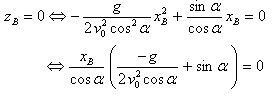
 Cette équation admet 2 solutions x_B = 0 ou

Or 2 sin α cos α = sin 2α