Licence 1 > Electrocinétique > Résumé de cours sur le condensateur et la bobine
EC2 : condensateur et bobine
L'essentiel
Condensateur
Un condensateur est constitué de deux armatures conductrices séparées par un isolant appelé diélectrique.
Les condensateurs sont caractérisés par leur capacité \(C\) qui s’exprime en Farad.
L’armature qui reçoit le courant porte la charge \(+q\).
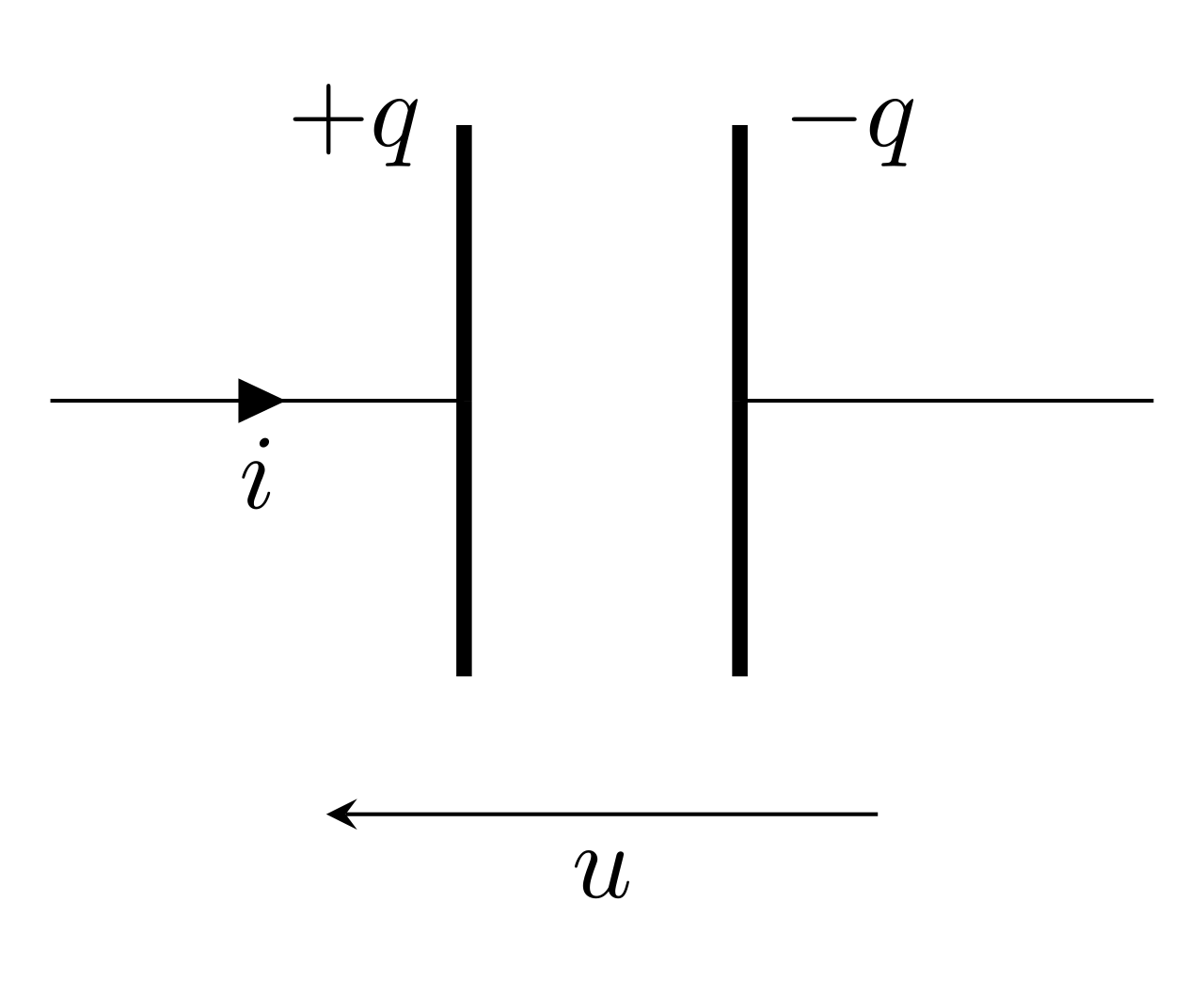
Relation intensité-tension pour le condensateur
\begin{equation*}\boxed{i=C\dfrac{\mathrm{d}u}{\mathrm{d}t}}\end{equation*}
Comportement du condensateur
Le condensateur se comporte en régime permanent comme un interrupteur ouvert. Il a donc un intérêt particulier en régime variable (transitoire ou permanent).
Énergie emmagasinée par un condensateur
\begin{equation*}\boxed{E_C = \dfrac{1}{2}\,C\,u^2}\end{equation*}
Un transfert d’énergie ne pouvant pas se faire instantanément, la tension \(u(t)\) aux bornes du condensateur est une fonction continue du temps.
Associations de condensateurs
En série
\begin{equation*}\boxed{\dfrac{1}{C_{eq}} = \dfrac{1}{C_1} + \dfrac{1}{C_2} + \dfrac{1}{C_3}}\end{equation*}
En dérivation
\begin{equation*}\boxed{C_{eq} = C_1 + C_2 + C_3}\end{equation*}
Bobine
Une bobine est constituée d’un enroulement de spires conductrices autour d’un isolant.
Elle est caractérisée par une inductance \(L\) exprimée en Henry et une résistance \(r\) exprimée en \(\Omega\).
Relation tension-intensité pour la bobine
\begin{equation*}\boxed{u = L\dfrac{\mathrm{d}i}{\mathrm{d}t} + r\,i}\end{equation*}
Comportement du bobine
La bobine se comporte en régime permanent comme un conducteur ohmique de faible résistance. Elle a donc un intérêt particulier en régime variable (transitoire ou permanent).
Énergie emmagasinée par la bobine
\begin{equation*}\boxed{E_L = \dfrac{1}{2}\,L\,i^2}\end{equation*}
Un transfert d’énergie ne pouvant pas se faire instantanément, l’intensité \(i(t)\) qui circule dans la bobine est une fonction continue du temps.
Associations de bobines
En série
Une association de \(n\) bobines réelles identiques caractérisées par le couple \(L,r\) est équivalente à une bobine d’inductance \(nL\) associée à un conducteur ohmique de résistance \(n\,r\).
En dérivation
Pour deux bobines idéales d’inductance \(L_1\) et \(L_2\) :
\begin{equation*}\boxed{\dfrac{1}{L_{eq}}=\dfrac{1}{L_1}+\dfrac{1}{L_2}}\end{equation*}
Différents types de régimes
Régime continu : toutes les grandeurs électriques sont constantes au cours du temps.
Régime variable : ces grandeurs dépendent du temps.
Régime permanent : pendant un certain temps, les caractéristiques des grandeurs électriques ne sont pas modifiées. Un régime variable comme le régime sinusoïdal est permanent : les grandeurs varient mais périodiquement.
Régime transitoire : c’est un régime de transition entre deux régimes transitoires. Sa durée est souvent courte.
Echelon de tension
Il y a échelon de tension lorsque la tension passe brutalement d’une valeur \(E_1\) à une valeur \(E_2\).
Un GBF réglé pour délivrer une tension créneau périodique soumet le circuit de charge à des échelons de tension successifs.
Circuit RC soumis à une tension : équation différentielle
\begin{equation*}\boxed{\tau\dfrac{\mathrm{d}u}{\mathrm{d}t}+u = e}\end{equation*}
Charge du condensateur soumis à un échelon de tension
Tension aux bornes du condensateur
On soumet le circuit RC à un échelon de tension d’amplitude E : La tension aux bornes du condensateur qui se charge s’écrit :
\begin{equation*}\boxed{u(t) = E \left(1 - e^{-\frac{t}{\tau}}\right)}\end{equation*}
Et son allure est représentée ci-contre. On peut vérifier que la fonction \(u(t)\) est bien continue.
Cette figure montre également comment obtenir la constante de temps \(\tau\).
Intensité du courant dans le circuit
\begin{equation*}\boxed{i(t) = \dfrac{E}{R} e^{-\frac{t}{\tau}}}\end{equation*}
La fonction \(i(t)\) est discontinue.
Décharge du condensateur soumis à un échelon de tension
Tension aux bornes du condensateur
La tension aux bornes du condensateur qui se décharge s’écrit :
\begin{equation*}\boxed{u(t) = E e^{-\frac{t}{\tau}}}\end{equation*}
Et son allure est représentée ci-contre. On peut vérifier que la fonction \(u(t)\) est bien continue.
Intensité du courant dans le circuit
\begin{equation*}\boxed{i(t) = - \dfrac{E}{R} e^{-\frac{t}{\tau}}}\end{equation*}
La fonction \(i(t)\) est discontinue.
Circuit RC : aspect énergétique
En travaillant l’équation différentielle concernant ce circuit, on peut obtenir :
\begin{equation*}Ri^2\mathrm{d}t + \mathrm{d}\left(\dfrac{q^2}{2C}\right) = e\,i\,\mathrm{d}t\end{equation*}
Cette équation fournit alors un bilan énergétique :
\(Ri^2dt\) correspond à l’énergie dissipée par effet Joule dans le conducteur ohmique pendant le temps \(\mathrm{d}t\) ;
\(\mathrm{d}\left(\dfrac{q^2}{2C}\right)\) correspond à l’énergie stockée dans le condensateur pendant le temps \(\mathrm{d}t\) ;
\(eidt\) correspond à l’énergie fournie par la source de tension pendant le temps \(\mathrm{d}t\).
A partir de cette équation, on peut montrer que la moitié de l’énergie fournie par le générateur est stockée dans le condensateur et que l’autre moitié est dissipée par effet Joule dans le conducteur ohmique.
Lors de la décharge du condensateur, il y a dissipation de l’énergie stockée dans celui-ci dans le conducteur ohmique.
Circuit RL soumis à une tension : équation différentielle
\begin{equation*}\boxed{\tau\dfrac{\mathrm{d}i}{\mathrm{d}t} + i = \dfrac{e}{R}}\end{equation*}
Etablissement du courant dans le circuit RL soumis à un échelon de tension
Courant dans le circuit
\begin{equation*}\boxed{i(t) = \dfrac{E}{R} \left(1 - e^{-\frac{t}{\tau}}\right)}\end{equation*}
Et son allure est représentée ci-contre. On peut vérifier que la fonction \(i(t)\) est bien continue.
Aussi, on voit qu’il est aisé de trouver la constante de temps \(\tau\) du circuit.
Tension aux bornes de la bobine lors de l’établissement du courant
\begin{equation*}\boxed{u(t) = E e^{-\frac{t}{\tau}}}\end{equation*}
La fonction \(u(t)\) est discontinue.
Rupture du courant dans le circuit
Courant dans le circuit
\begin{equation*}\boxed{i(t) = \dfrac{E}{R} e^{-\frac{t}{\tau}}}\end{equation*}
Et son allure est représentée ci-contre. On peut vérifier que la fonction \(i(t)\) est continue.
Tension aux bornes de la bobine lors de la rupture du courant
\begin{equation*}\boxed{u(t) = - E e^{-\frac{t}{\tau}}}\end{equation*}
La fonction \(u(t)\) est discontinue.
Circuit RL : aspect énergétique
Comme pour le circuit RC, on peut montrer que lors de l’établissement complet du courant dans le circuit, la moitié de l’énergie fournit par le générateur est stockée dans la bobine sous forme magnétique, l’autre moitié est dissipée par effet Joule.
Lors de la rupture du courant, l’énergie stockée dans la bobine est intégralement convertie et perdue par effet Joule dans le conducteur ohmique.


